Remarks

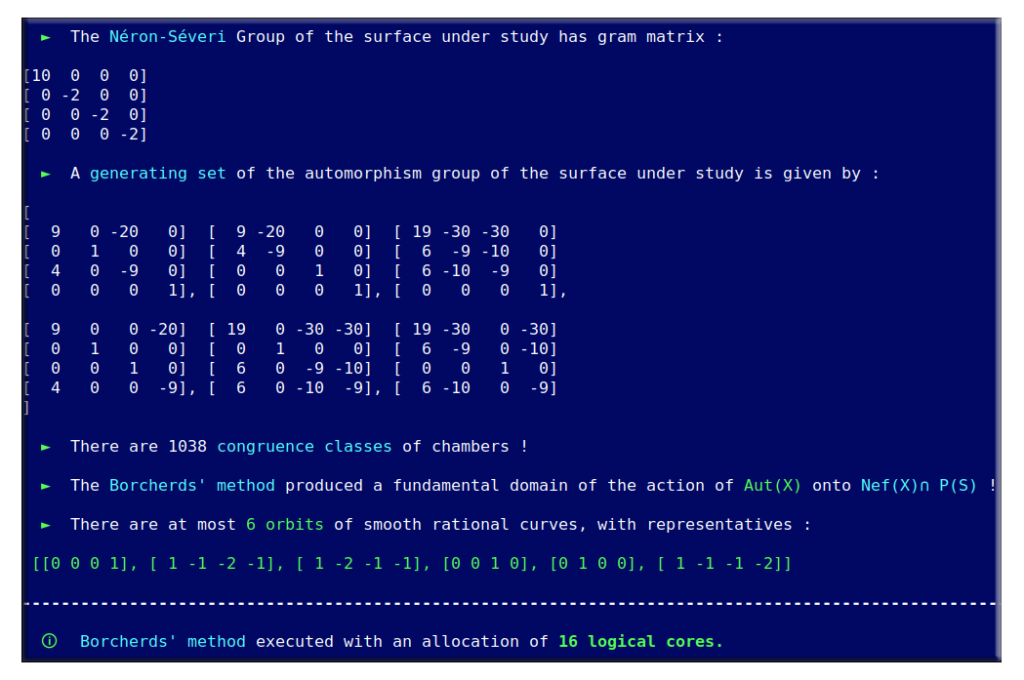
On this page, we formulate various remarks and display screenshots depicting some of the tools produced during this thesis.

Note that programs are here executed directly within Sage’s Python environment and will be publicly released after the defense.

Note that the goal defined by our advisor regarding this thesis was the study of a family of surfaces and in no way the implementation of computer-based solutions to do so.

Regarding the study of automorphism groups, Shimada gave a new life to the thirty-year-old Borcherds’ method almost a decade ago. Since then, this approach has not known any development. There was, however, a huge opportunity that could be seized by using a computer-based algorithmic approach as a means to fulfill our goals for this thesis.

To deal with the Borcherds’ method while building on the work done in 2013 by Shimada, we proceeded according to the following course of action :

  • Point 1 – We first had to recontextualize the Borcherds’ method in a setting from which a general application framework could be identified.

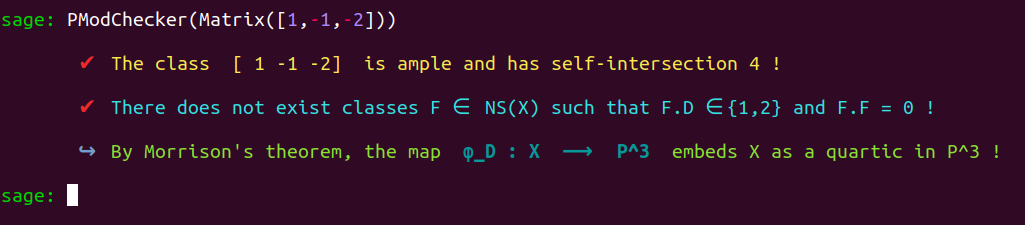
That is: What conditions should be satisfied by a complex $K3$ surface $X$ to obtain a generating set of $\text{Aut}(X)$ by applying the Borcherds’ method? Can we determine whether these conditions hold with a minimal amount of input data to make a 100% automatized implementation of the method?

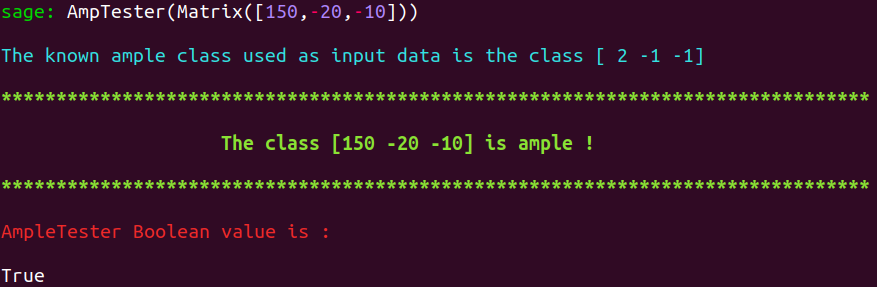
Both of these interrogations have a positive answer. We precisely identified such conditions and produced programs to test whether they hold.

From the only input data of an ample class, of the Gram matrix of the Néron-Severi lattice of your K3 surface, and of vectors providing a primitive embedding of this lattice into a suitable even hyperbolic ambient lattice (specify the vectors, the program will take care of choosing the ambient lattice) depending on the Picard number of the surface under study, you will be able to execute our implementations with 100% automation if the surface has Picard number inferior or equal to $17$. Following the goals initially defined for this thesis by our advisor, we focused on the study of $K3$ surfaces of small Picard number and infinite automorphism group. Had we been tasked with studying surfaces of higher Picard numbers, we would have rewritten all our code in C++ to ensure optimal efficiency. The result would undoubtedly be less handy, but even more massive performance gains can be obtained this way.

NB: Python code is compiled to bytecode and then interpreted by a VM… While C++ code is compiled into binary code, which can then be directly executed by the CPU… Hence, Python (and thus all the SageMath stuff) is NOT the way to go if you have HPC in mind. You can recycle what we have done in C++ to obtain massive gains in terms of performance. Moreover, note that all the Sage functions & integrated features we used can be easily transposed outside of a Python environment (take a look at Sage’s source code).

  • Point 2: In this context, we took advantage of all the building blocks provided by Shimada 10 years ago and then filled all the gaps which had been left in the wake of his article.

We had to work on a generalized embedding update procedure, a generalized membership criterion to identify automorphisms, and a concrete and generalized criterion to determine whether the Borcherds’ method can be applied to a given complex K3 surface and return a generating set of the automorphism group…

Once these two essential preliminary points had been addressed, we could start modernizing the various procedures and the method itself (optimization, parallelization, etc.) while always using mainstream tools without looking at things in terms of HPC.

Please make no mistake; this thesis has nothing to do with High-performance computing. We tried to make the best possible use of the tools we had on hand.

The simple algorithmic structure of the classical Borcherds’ method exhibits obvious critical points on which enforcing modern tools could bring huge improvements. We, of course, took advantage of each one of the resulting opportunities. For example, here is described a situation in which the benefits of using a modern solution such as parallelism are apparent!

The version of the Borcherds’ method used to obtain the results displayed on this page is the Poolized Borcherds’ method, which takes advantage of process-based parallelism at the scale of the internal building blocks of the Borcherds method (e.g., for congruence testing). We use the Pool object from the Python 3 multiprocessing library to do so.

In section 1.11 of our thesis, “Towards a parallelized Borcherds’ method,” we deal with the challenge of also enforcing parallelism at the level of the Borcherds’ method itself while still keeping the ability to take advantage of “all-in-one” solutions such as Pool for to deploy the internal procedures of the method in parallel!

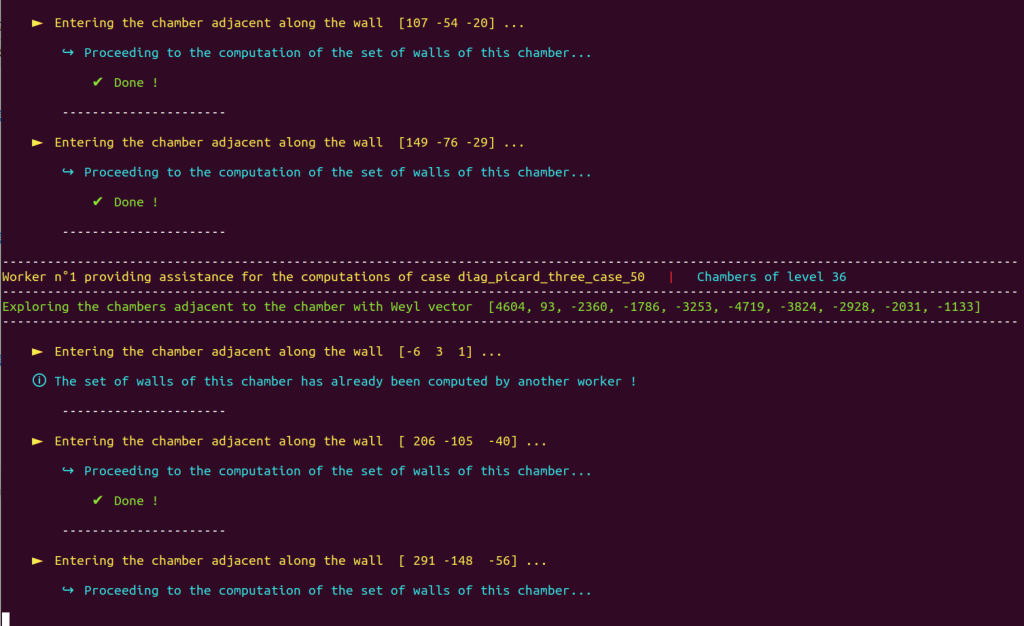
Doing so consists, for example, distributing over various worker processes the burden of the exploration of the chamber structure and the computation of the sets of walls of each chamber explored during each iteration.

Thus, we produced a fully functional worker (autonomous Poolized Functional block) that can be deployed in parallel over several processes. All workers communicate through a common database and work to benefit a primary process.

The latter is also capable of mobilizing at the same time another Pool of workers to execute CongChecker blocks and speed-up congruence testing.

We hope that in the future, this work will enable people who may be working on improving the Borcherds’ method to save time.

Also, note that our implementations are done in Python and heavily rely on functions from the Sage library. Doing so comes at a price in terms of raw performance.

If you have genuine high-performance computing in mind, there is without any doubt a lot of room for improvement in terms of performance. However, we enter on a ground that has nothing to do with this thesis.

The reader should note that we always work according to the following principles :

  • The KISS principle: Keep It Simple, Stupid.
  • If it ain’t broke, don’t fix it.
  • Prioritize & Execute.

Thus, we used mainstream, accessible, popular modern tools and followed a pragmatic approach. We’re not ones to pretend to be geniuses trying to reinvent the wheel, especially when dealing with basic principles of process-based parallelism.

Hence the following illustration regarding parallelism at the scale of the Borcherds’ method itself :

Above is an illustration of the enforcement of parallelism at the scale of Borcherds’ method. One can imagine that the primary Borcherds process is the giant Hamster. It explores and processes all the red chambers adjacent to yellow chambers. The smaller hamsters are Borcherds’ worker processes and work in sync to benefit the primary process. They compute the sets of walls of red chambers which have been specifically assigned to each of them and enable the primary process to directly retrieve the data of these sets of walls when it is needed, thus minimizing the workload over the shoulders of the master process in terms of computation of sets of walls…
Poolized Borcherds worker APFB assisting an instance of the Poolized Borcherds’ method augmented with a Poolized Functional Block. At its core, a Borcherds’ worker is simply an autonomous Poolized functional block. The Poolized Borcherds’ worker can be executed on as many processes as desired by the user. There is more: If you have access to a shared storage solution (e.g., a shared folder) you can execute the Borcherds’ method on as many computers as you want to study a given surface! More generally, all our programs possess a recovery feature… In case your computer crashes for some reason or a computation is interrupted, the data will automatically be retrieved at the next start of the program, and computations will restart from the point from which they were stopped. For example, suppose computer n°1 has a CPU with 32 logical cores. In that case, you could safely launch a Borcherds’ primary process with an allocation of 16 cores and two Borcherds’ workers with an allocation of 8 cores each on computer n°1. If computer n°2 has eight cores, you can launch another Borcherds APFB worker with an allocation of 8 cores if you want, and so on… The concept is simple: all workers work for the benefit of the primary process, all workers are capable of deploying process-based parallelism for their own work, and all workers always keep an eye on the shared database to avoid computing a set of walls that have already been computer by another worker! Note that the standalone Poolized Borcherds’ method will be enough to deal with most cases of small Picard number quickly. That’s why we use it most of the time.

Note that we used the Poolized Borcherds’ method to obtain the following results.

That is, we used an implementation of the Borcherds’ method, which can deploy its internal procedures in parallel: Parallelism is used at an internal level.

Note that making use of our implementation of Shimada’s classical Borcherds method (classical, but with many tweaks and optimizations, of course !) amounts to setting

nb_workers = 1

The value of nb_workers should not exceed the value of os.cpu_count()

Also, note that our Poolized Borcherds’ method possesses a recovery feature and can be paused or restarted from another machine if necessary. Thus, facing a power outage won’t have any consequences!

There is no need to start a heavy computation from zero again in such a situation!

Our Poolized Borcherds’ method integrates a Poolized functional block, thus making it fully compatible with as many Borcherds’ workers APFB as you want, which can be used to assist in the computations from any other machine.

The PFB/APFB approach can also be executed over a 100% cloud-based infrastructure.

Using the PFB / APFB approach is not necessary to obtain the following results in an acceptable time.

In practice, the level of performance reached by the standalone Poolized Borcherds method is acceptable for us. We have achieved massive gains over our very first implementations, so immense that we cannot quantify them.

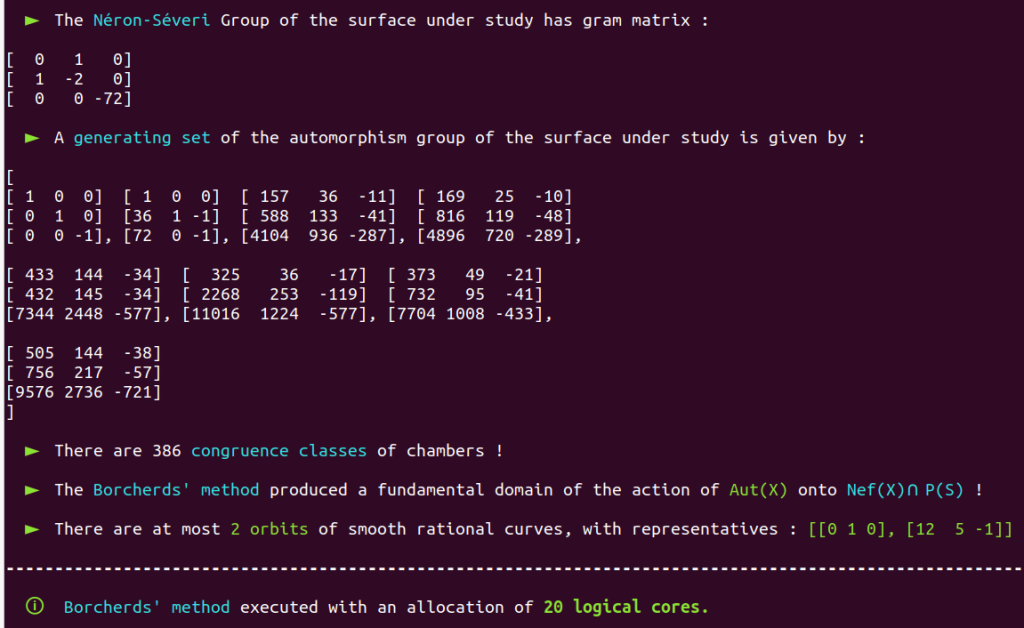
Remember that our thesis’ original goals consisted of studying a family of $K3$ surfaces of Picard number $3$… However, we could easily extend the study to larger Picard numbers.

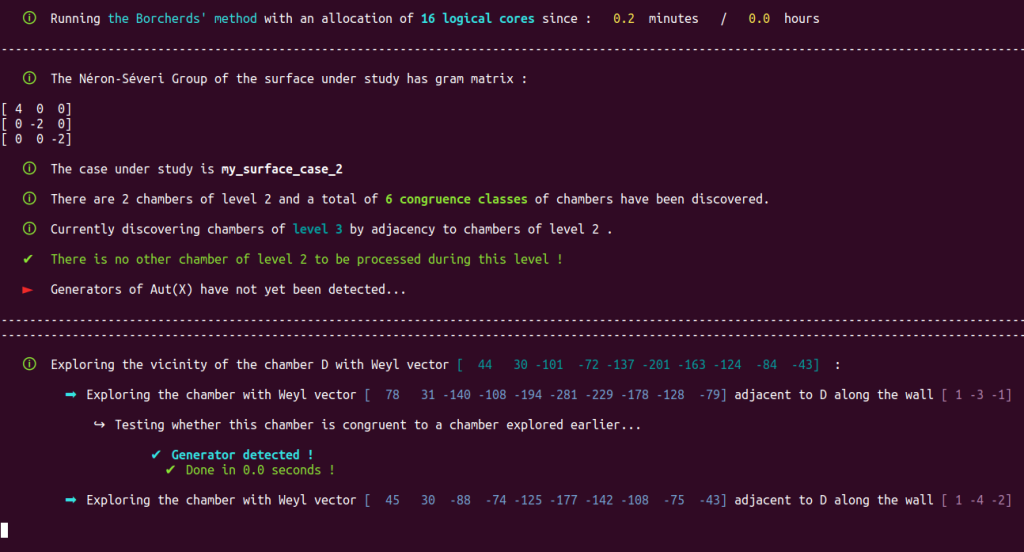
Our Poolized Borcherds’ method takes advantage of the console GUI to display in real-time the course of events that occur, e.g.

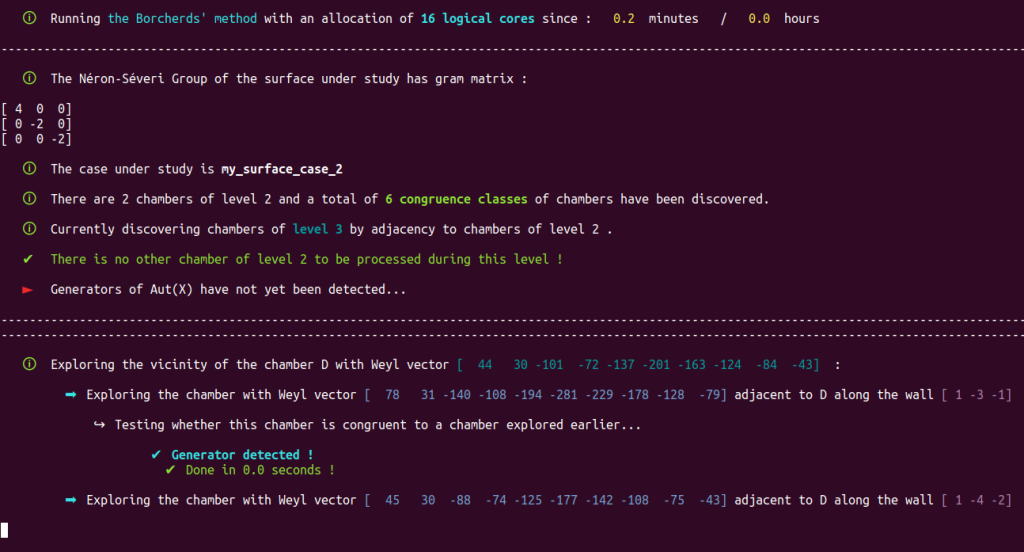
It also produces a lot of useful monitoring data in dedicated and real-time updated files. Note that automatically generated progress reports text files with time markers are also updated in real-time and included with the monitoring data produced by the Poolized Borcherds’ method: generators, congruences, $(-2)$-walls, data of the chambers explored, data of the representatives of congruence classes, etc.

One last thing: For convenience, we will provide all our solutions as Sage Programs, depicted as running within a Sage Python 3.8.5 console. However, one should remember that these Sage programs are simply Python programs taking advantage of the SageMath Python library and can be easily redeployed within another Python environment.

Execution of the Borcherds’ method completed, results are displayed.
This example illustrates that Borcherds’ method provides a non-minimal generating set of Aut(X). In this case, Aut(X) is generated by the first four matrices, as mentioned above. One can easily see that all the other so-called generators can be obtained from the data of the first four! One can quickly implement an algorithmic routine to directly refine the generating set produced by the Borcherds’ method.
Here is the Picard four version of the above-mentioned K3 surface. If you take a look back at the results in Picard five, you will see that the shape of the generators (the first four) in Picard 5 is naturally such that Aut(X) in Picard 5 contains all the information of Aut(X) in Picard 4. Indeed, this “diagonal” family of K3 surfaces has the property that the Néron-Severi of one of its members in a given Picard contains copies of the Néron-Severi groups of its little sisters of smaller Picard number.
In continuation to the two previous examples, here is the Picard 3 version of the surface mentioned above.
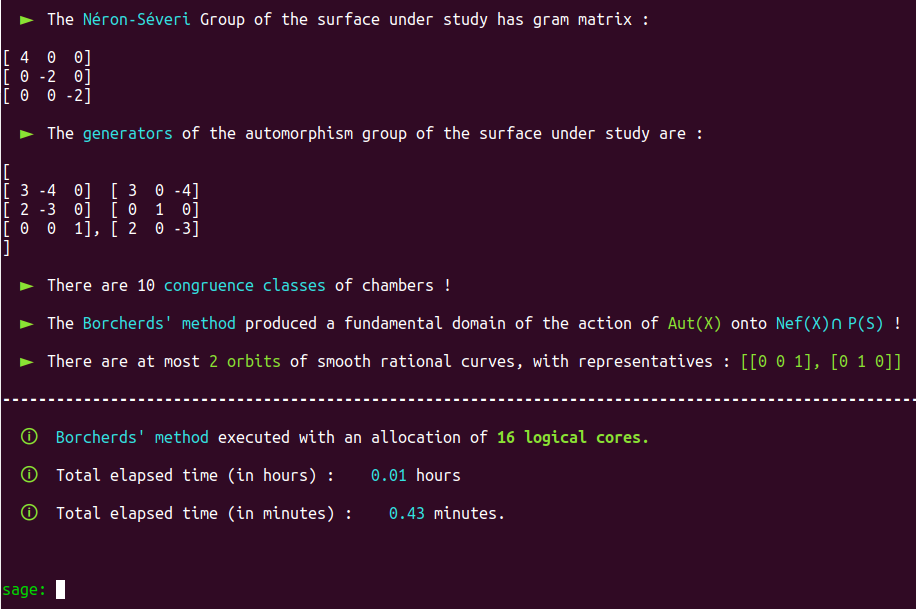
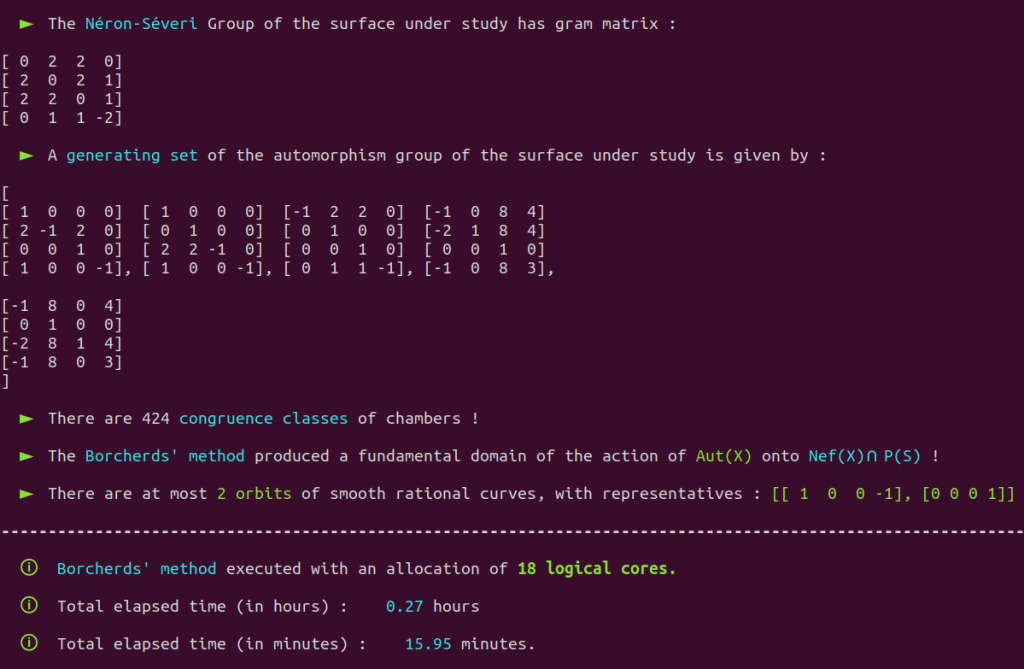
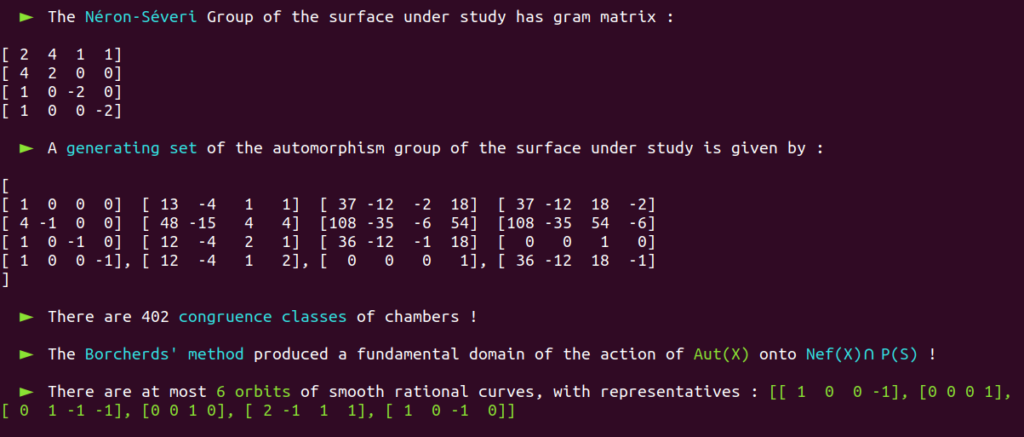
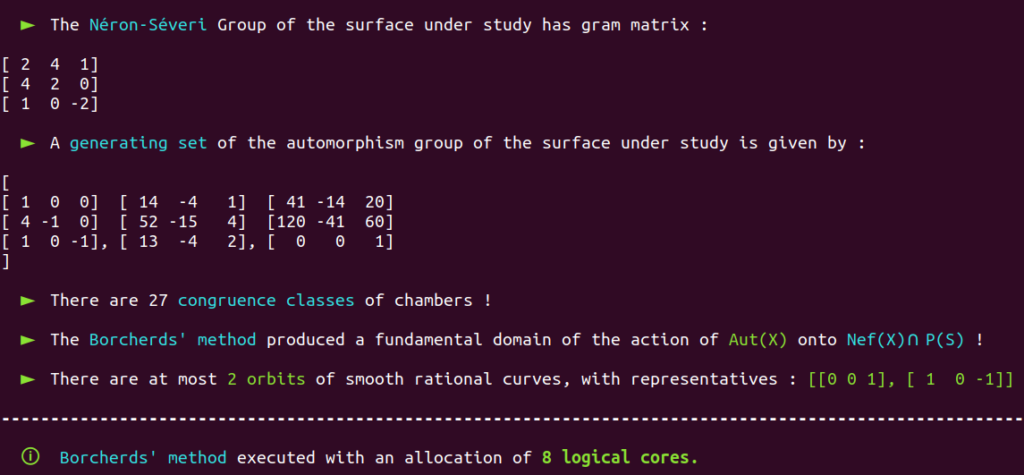
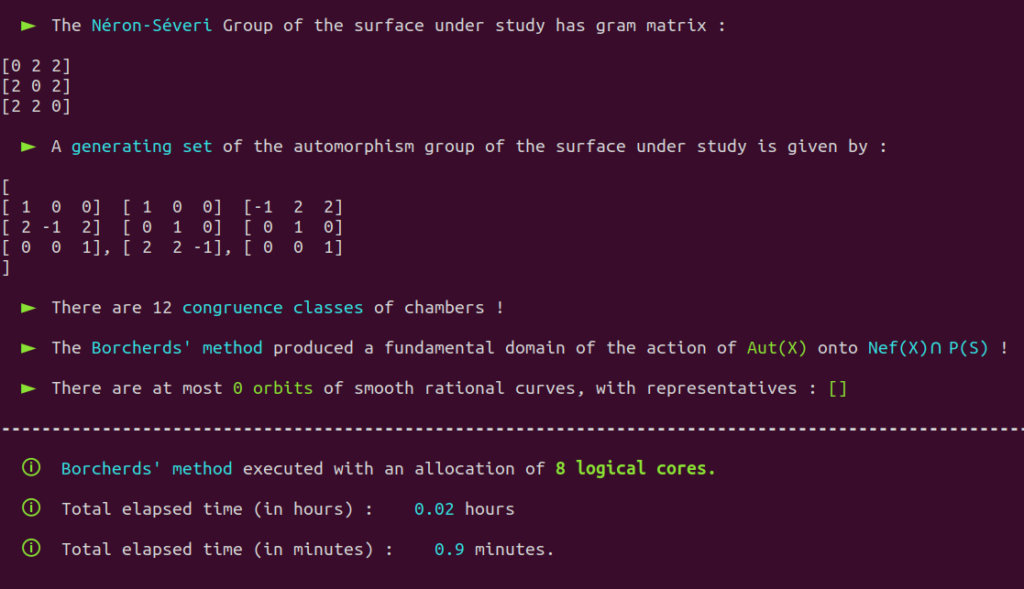
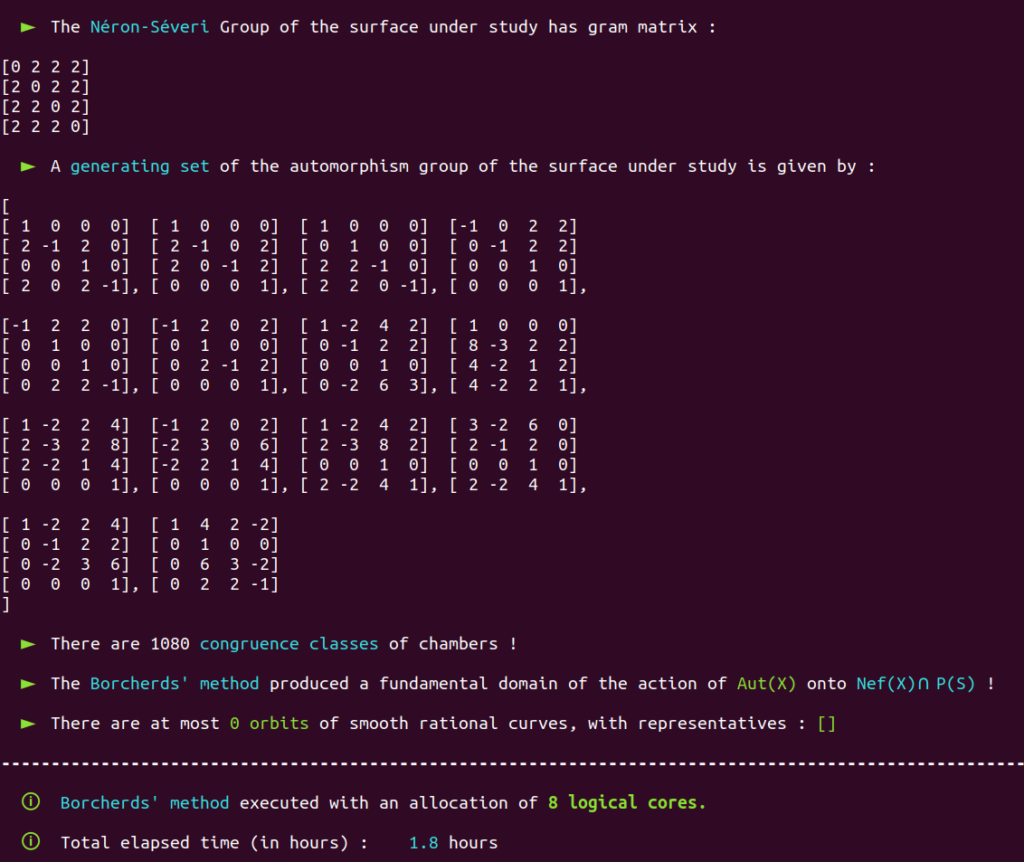
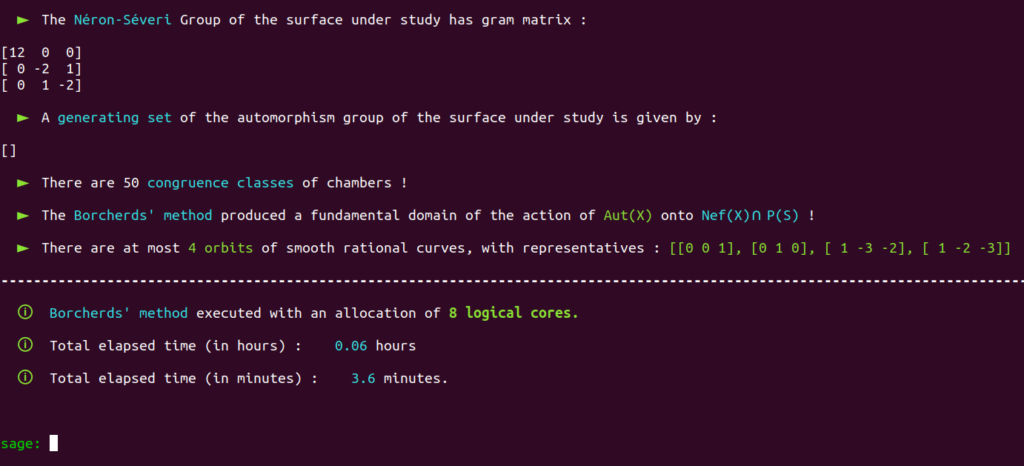
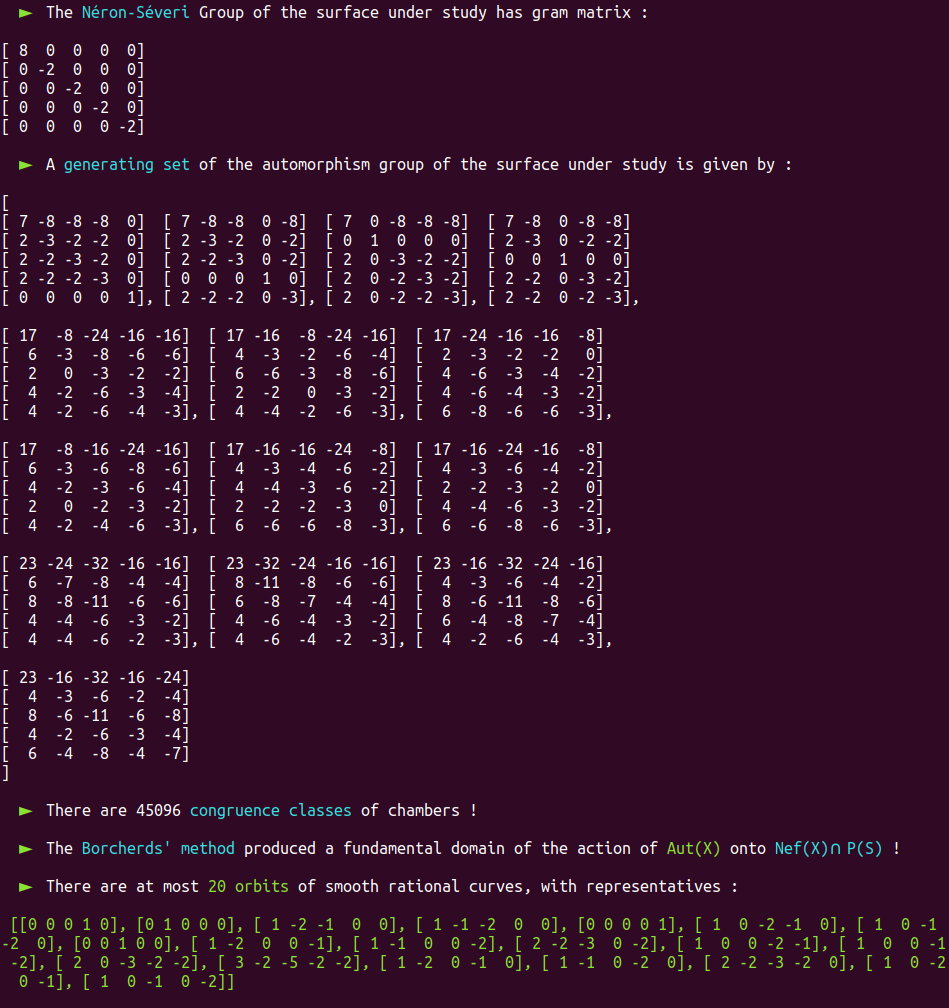
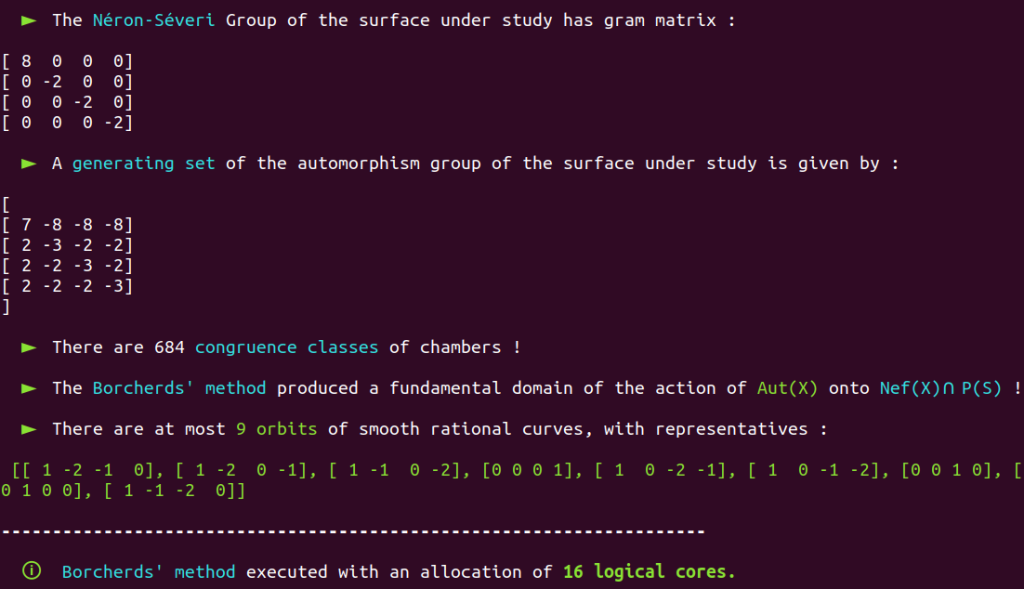
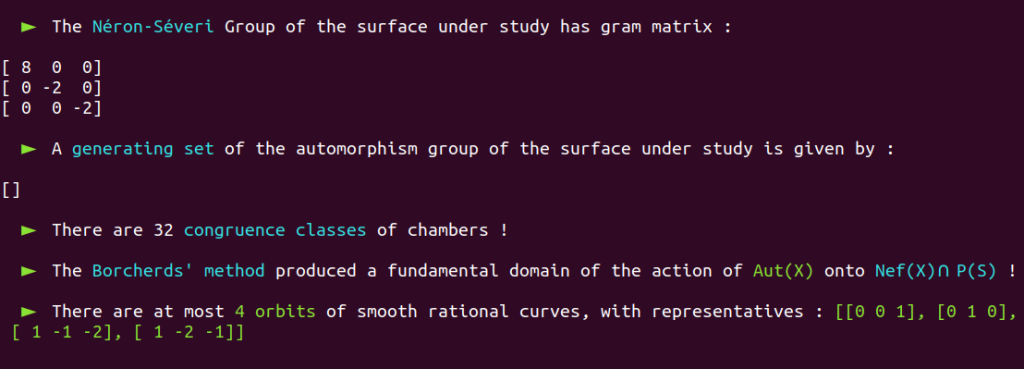
It is a well-known fact that the automorphism group of this surface has already been classified in the past.
To see this, look at Xavier Roulleau’s atlas of K3 surfaces with a finite automorphism group!
Aut(X) is trivial; there are only four classes of smooth rational curves on this surface, and thus four orbits!

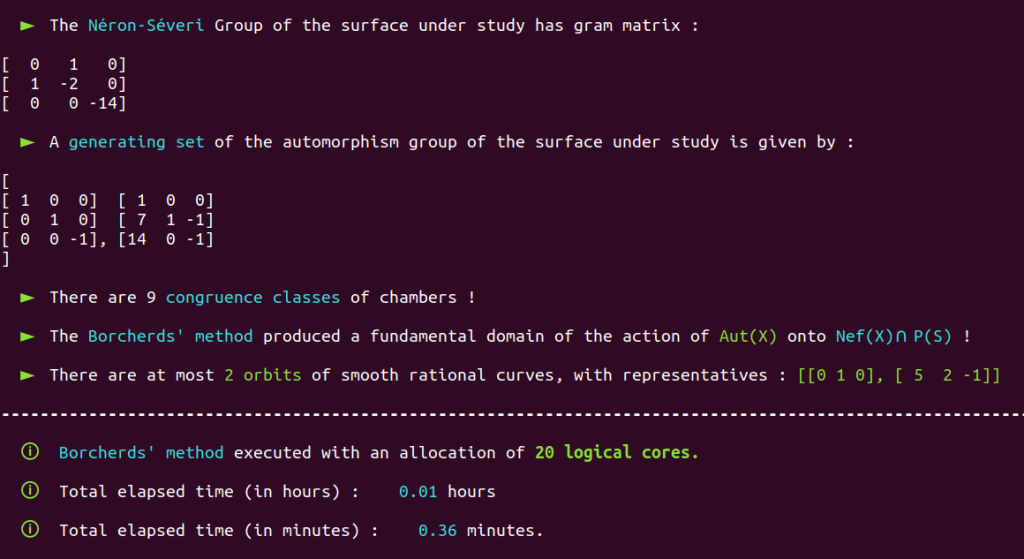
This case is Shimada’s surface, case k=7, from his paper
“An algorithm to compute automorphism…”
There is NO NEED to allocate so much processing power on a straightforward case like this!
More generally, doing so for cases in Picard 3 may even be counterproductive!
Here are the results for the case k=36 of the family of K3 surfaces studied by Shimada.
The Borcherds’ method running on a pretty straightforward case.
Universal tester for projective models, based on a famous theorem from Morrison.
Universal ampleness tester