The congruence testing procedure is without any doubt one of the most important procedures involved in the Borcherds’ method. Congruence testing is indeed the main lever of action at the disposal of the method in order to exhibit generators of $\text{Aut}_{\mathbf{H}}(\nps)$, which is isomorphic to $\aut(X)$ whenever the $K3$ under study meets the required conditions we already discussed inside of the PDF file of the thesis, section 1.6, and also on this website. In this online section, we show how to efficiently deploy congruence testing within the Borcherds’ using parallelism. Deploying procedures in parallel is, for sure, a worthy intention. It is however of paramount importance to make sure that such procedures are decently optimized for execution in series before moving on to parallel deployment. That is, we recommend that you at least try to optimize, i.e., try to improve procedures as much as possible, with efficiency in mind, before trying to redesign everything in terms of parallelism. This endeavor enables us to highlight an aspect of our work that has been overlooked in the PDF file of the thesis due to the limitations and constraints of the conventional format of a thesis manuscript.
Indeed, some of the improvements we brought to Prof. Shimada’s 2013 work are not really noticeable in the framework of $K3$ surfaces of small Picard number. Remember that such surfaces have been the initial object of study of this thesis, and the latter turned out to deal with subjects far beyond its initial scope and objectives. However, the value of these once overlooked improvements becomes obvious as soon as the surfaces under study are such that an execution of the Borcherds’ method involves tens of thousands, hundreds of thousands, or even millions of representatives of congruence classes of chambers. To show this, we use a simple example, involving 80231 representatives of chambers, and thus 80231 congruence tests.
These tests are first performed using Prof. Shimada’s 2013 approach and then performed by enforcing our 2022 approach regarding congruence testing. Note that the latter is first deployed in series, and in parallel, so this section gives us at the same time an opportunity to demonstrate how we used Pool on a concrete example.
| Approach | Total time needed to test a chamber $D$ for congruency against $80231$ chambers (averaged over at least $3$ runs of the $80231$ tests) | Remarks |
|---|---|---|
| 2013 approach | $\approx 2845$ seconds | We here make the assumption that congruence testing is performed in full compliance with the instructions found in Prof. Shimada’s 2013 article. |
| 2022 approach, no parallel deployment | $\approx 7$ seconds | $400$ times faster than the 2013 approach |
| 2022 approach, with parallel deployment (Pool) | $\approx 2.5$ seconds | more than $1000$ times faster than the 2013 approach |
NB1: We used the same programs, and the same environment, to perform all these experiments. That is, we did not “cheat” by using a sh*tty and slowed down implementation of the 2013 approach to make it look bad, to then use a radically different implementation to claim amazing improvements. Doing so would be unfair to the 2013 approach, and would go against the rules of ethics. When we write “2013 approach“, we mean that we followed exactly Prof. Shimada’s guidelines from his article; Algorithm 3.19 for congruence testing, and Algorithm 6.1 for the deployment of congruence testing.
NB2: Even better results will be obtained if you implement the method with High-Performance Computing in mind. The programs produced during this thesis SHOULD NOT be viewed as HPC compliant and have not been produced with any form of concern for HPC. We wouldn’t have used Python & SageMath if HPC had been our goal. The parallel aspect of our work is due to the fact that AMU & AMidex enabled us to obtain an additional full year of funding in order for us to write our thesis in the best possible conditions instead of rushing to deliver a messed-up PDF file and defend the thesis in September or October 2021, as was originally planned. It turned out that this additional year enabled us to not only deliver the PDF file but also to produce new content, outside of the scope of the thesis.
This thesis, however, may help people to produce an HPC version of all the programs without hassle. At worse, this thesis should at least make things easier for people to do so. Making sure that this thesis can be used by other people as a gateway for the future of the Borcherds’ method has always been one of our goals.
The reader may be wondering
What is the trick? WTF?
There is no trick. We used the same technique that we used to derive the $-1 \notin \ker(\eta_T)$ criterion which enabled us to identify a general framework of application for the Borcherds’ method, and implement programs which automatically determine whether the method can be applied to a given surface and return a gen. set of $\aut(X)$.
That is, we used basic logic, and rules of inference, again. More precisely, in the current situation, we derived a criterion that, given a chamber $D$ to be tested against each chamber of a given list of chambers, can be implemented on a computer and enables us to rigorously identify most of the chambers in the given list which cannot be congruent to $D$. We use the two following facts, which can both be inferred using basic logic from the notions of congruency and sets of walls :
Fact 1
Two chambers $D_1$ and $D_2$ that do not have the same number of walls, i.e., such that $$\text{Card}(\Omega(D_1))\neq \text{Card}(\Omega(D_2))$$ cannot be congruent !
Fact 2
If the respective sets of squares of elements of $\Omega(D_1)$ and of $\Omega(D_2)$
do not coincide, i.e., if $$\{ \langle u , u\rangle_{S^\vee} \mid u\in \Omega(D_1) \} \neq\{ \langle u , u\rangle_{S^\vee} \mid u\in \Omega(D_2) \}$$ then $D_1$ and $D_2$
cannot be congruent !
Note that for any $\ps$-chamber $D$ the elements $v\in \sv $of $\Omega(D)$ have square satisfying $$ -2\leq \langle v,v\rangle <0$$ by design of the Algorithm 5.8 (procedure DeltaW in our thesis) due to Professor Shimada.
Thus, there is no need to check for equality of squares in $\QQ / 2\ZZ$ in the above fact 2. That’s why we just check for equality in $\QQ$ in the code.
Regarding our example involving 80231 congruence tests, we will see that we avoid the annoyance of having to perform
99,97%
of these tests thanks to a criterion obtained by combining the facts $1$ and $2$, which, as we will see, costs almost nothing in terms of computation time and resources, when executed. That is, 80208 tests out of the 80231 are shown to be negative without having to be performed…
This criterion is a GAME-CHANGER for the study of surfaces of higher Picard number and which involve huge numbers of representatives of congruence classes during the execution of the Borcherds’ method. It should not be overlooked.
Assume that we have to test for congruence a chamber $D^\prime$ against all the known representatives of congruence classes, that is, we assume that we have to test $D$ for congruence against each $$D^{\prime \prime} \in \bigcup \mathbb{D}^\ast.$$ We introduce a procedure CongDodger which takes as input the set $\bigcup \mathbb{D}^\ast$, identifies the elements $D^{\prime \prime}$ such that
$$\text{Card}(\Omega(D^{\prime\prime}))\neq \text{Card}(\Omega(D^\prime))$$
and removes them from $\bigcup \mathbb{D}^\ast$. The procedure CongDodger then outputs a set $$( \bigcup \mathbb{D}^\ast)^\flat$$ from which such elements have been removed. This is how we implemented the above-mentioned Fact 1.
We then test for congruence $D^\prime$ against each $$D^{\prime \prime} \in ( \bigcup \mathbb{D}^\ast)^\flat$$ with the procedure CongChecker. The latter integrates an if control sequence at its beginning, which, given the input of the sets of walls of $D^\prime$ and of a chamber $D^{\prime \prime}$, checks whether the square of the elements in their respective sets of walls coincide. When this is the case, CongChecker performs the congruence test. When the sets of squares are not equal, CongChecker directly returns false, and thus does not perform the congruence test of $D^\prime$ against $D^{\prime \prime}$ since these chambers cannot be congruent.
In order not to overburden things, we did not focus on this aspect of our approach in the PDF file of the thesis. The structure of an iteration of the Poolized Borcherds’ method, should, in fact, be represented as follows :
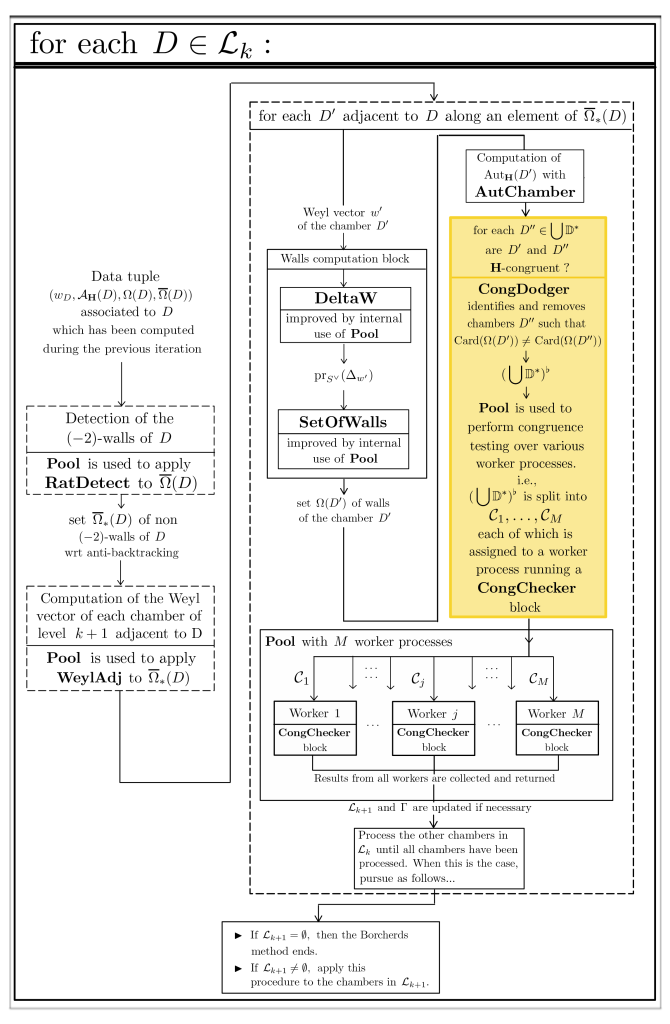
We will start by performing congruence testing by following to the letter the instructions & guidelines which can be found in Professor Shimada’s 2013 article. Our implementation of Prof. Shimada’s 2013 procedure is named CongCheckerOriginal. We will then take a step back and show see that major improvements can be brought to Prof. Shimada’s original approach to congruence testing, with a huge reduction in computation times. The resulting procedure is CongChecker (and is, in particular, suitable for parallel deployment). In fact, we rigorously show using basic logic and inference rules that Professor Shimada’s approach of congruence testing can be greatly improved, as indicated earlier: We use as an example a situation that occurs at the end of the execution of the Borcherds’ method to compute a generating set of the automorphism group of a $K3$ surface. In the framework of this example, following Professor Shimada’s 2013 approach leads us to perform $80231$ congruence tests. As announced at the beginning of this section, we will rigorously show that $99.97\%$ of these tests are superfluous so that only $23$ congruence tests have to be performed.
We will then show how to enforce congruence testing in parallel with Pool to take advantage from process-based parallelism.
Please note that we will illustrate the material from points 1, 2, and 3 on the real-life example of the $K3$ surface $X_5$ in Picard number five. Compared to the 2013 approach mentioned in point $1$, we will see that computation times are approx. 400x faster when we use the approach mentioned in point 2, and more than 1000x faster when we combine the approaches mentioned in points 2 and 3. The $K3$ surface $X_5$ has Néron-Severi group $S=\NSX$ isomorphic to the integral lattice with Gram matrix $$ G_S=\begin{bmatrix} 10 & 0 & 0 & 0 & 0 \\
0 & -2 & 0 & 0 & 0 \\
0 & 0 & -2 & 0 & 0 \\
0 & 0 & 0 & -2 & 0 \\
0 & 0 & 0 & 0 & -2 \end{bmatrix}$$
A generating set of $\aut(X_5)$ can be found by clicking here.
Starting from the standard initial $\ps$-chamber $D_0$ induced by the $\pl$-chamber $\DD_0$ with Weyl vector
$$ [31 , 30 , -68 , -46 , -91 , -135 , -110 , -84 , -57 , -29],$$ the Borcherds’ method enables us to compute the above mentioned generating set for $\aut(X_5)$ and produce a complete set of representatives of congruences classes of chambers contained in $\nps$ made of a total of $80232$ chambers layered into 55 levels, from the level zero to the level 54. As indicated in the thesis, we use the standard basis for $S^\vee$ obtained by taking the columns of $G_S^{-1}$ in order to express coordinates of elements having an orthogonal complement in $\ps$ inducing walls of chambers whenever such elements have to be used as input data for procedures such as CongChecker or AutChamber. Open a Sage session in the folder ThesisPrograms and execute the following code, which sets up the initial environment necessary to study $X_5$ :
INPUT_DATA=load('INPUT_DATA/DIAG_PICARD_FIVE/INPUT_DATA_xt_picard_FIVE_case_5.sobj')
load('init_emb.sage')
load('emb_updater.sage')
load('degentest.sage')
TEST_CHAMBER=load('test_chamber_demo.sobj')
LIST_REPS_CONG_CLASSES = load('list_cong_classes_of_chambers_demo.sobj')
load('cong_demo.sage')We assume that the Borcherds’ method enters the chamber $D$ with Weyl vector
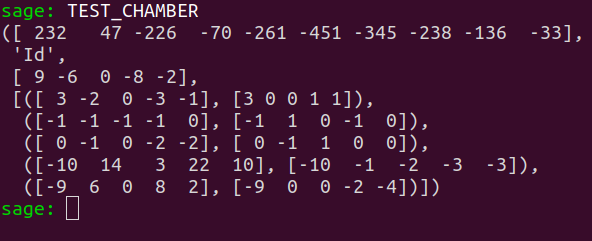
$$ [232 ,47 ,-226 ,-70 ,-261, -451, -345, -238, -136, -33]$$ computes its set of walls, a generating set of $\aut_{hbf}(D)$, and is ready to test $D$ for congruency against the $80231$ representatives of chambers discovered since the beginning of its execution.
The data associated with the chamber $D$ is contained in the list TEST_CHAMBER
The list LIST_REPS_CONG_CLASSES contains the data associated with representatives of congruence classes of chambers contained in $\nps$ and identified by the Borcherds’ method during its execution up to level 53.
Thus, LIST_REPS_CONG_CLASSES contains $80231$ chambers.
len(LIST_REPS_CONG_CLASSES) 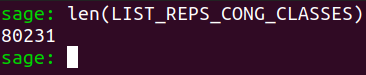
We introduce two congruence testing functions :
CongCheckerOriginal: The code behind this function results from a straightforward implementation of Professor Shimada’s congruence testing procedure described as mentioned in the description of his Algorithm 3.19 from his 2013 article. We will use this function in full compliance with what is indicated by Professor Shimada’s in his article.
CongChecker: This function, based on CongCheckerOriginal, is the result of an effort made during our thesis to perform congruence testing with efficiency and common sense in mind while abiding by Shimada’s logical structure. We will see that CongChecker enables us to deal with the congruence tests of the example under study 400x faster than CongCheckerOriginal when deployed in series, and more than 1000x faster than CongCheckerOriginal when deployed in parallel.
Let’s test $D$ for congruency against the $80231$ chambers in LIST_REPS_CONG_CLASSES by using Professor Shimada’s 2013 approach to the letter. To this end, we strictly follow his guidelines: CongCheckerOriginal is in line with Prof. Shimada’s Algorithm 3.19 and deployed in total compliance with Prof. Shimada’s algorithm 6.1. Note that CongCheckerOriginal is thus deployed in series, no parallelism is involved here. We perform this experiment by using timeit.repeat to time and perform this experiment three consecutive times. More info about timeit can be found by clicking here.
We will then consider the average time obtained from the times measured for the three consecutive trials. We enter
test_code_CongCheckerOriginal = """
CONG_TEST_RESULTS = []
for qqq in LIST_REPS_CONG_CLASSES :
CONG_TEST_RESULTS.append(CongCheckerOriginal([q[1] for q in TEST_CHAMBER[3]],[q[1] for q in qqq[3]],qqq[0]))
"""and run
times_CongCheckerOriginal = timeit.repeat(stmt = test_code_CongCheckerOriginal,globals=globals(),number=1,repeat=3) 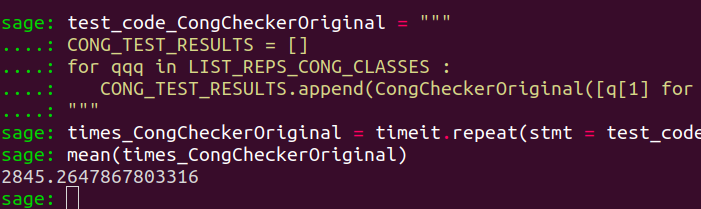
We obtain that on average, performing the 80231 congruence tests with CongCheckerOld, i.e., by following Prof. Shimada’s 2013 guidelines, took
$2845$ seconds.
This is neither sustainable nor acceptable.
What if we told you that performing the entirety of the 80231 congruence tests is not necessary?
Assume that two chambers $D_1$ and $D_2$ are congruent. Then there exists an element $g\in \hbf$ such that $D_{1}^{g} = D_2$. Then, as indicated by Prof. Shimada in his description of the congruence testing procedure (see his Algorithm 3.19), and as implied by the notion of congruency, the element $g$ establishes a bijection between the sets of walls $\Omega(D_1)$ and $\Omega(D_2)$ of these two chambers.
This implies that $\Omega(D_1)$ and $\Omega(D_2)$ have the same cardinality.
Do you see where we wanna go? Guided by common sense and basic inference principles, we take the contrapositive of the overall implication and obtain that :
Two chambers $D_1$ and $D_2$ that do not have the same number of walls, i.e., such that $$\text{Card}(\Omega(D_1))\neq \text{Card}(\Omega(D_2))$$ cannot be congruent !
We go back to our concrete example and see that testing $D$ for congruence against chambers that does not have the same number of walls as $D$ is superfluous, useless, and a pure waste of resources!
Indeed, we established above that testing such chambers for congruency against $D$ is not necessary, since the fact that they do not have the same number of walls as $D$ ensures that they cannot be congruent to $D$.
We, therefore, define the list of chambers, which, among the 80231 chambers, have the same number of walls as $D$ :
TO_BE_TESTED_SAME_NBR_WALLS=[qq for qq in LIST_REPS_CONG_CLASSES if len(qq[3])==len(TEST_CHAMBER[3])] Again, we note that chambers in LIST_REPS_CONG_CLASSES that do not belong to this list cannot be congruent to $D$.
We see that using basic inference and logic enabled us to significantly ease the burden of testing $D$ for congruence against the known representatives of congruence classes :

The number of representatives against which we have to test $D$ for congruency has been
lowered from $80231$ to $60287$ chambers!
It is not over, there is even better!
Again, assume given two chambers $D_1$, $D_2$, which are here assumed to be congruent. That is, there exists $g\in \hbf$ such that $D_{1}^{g} = D_2$. In particular, the element $g$ establishes a bijection between $\Omega(D_1)$ and $\Omega(D_2)$.
That is, for all $v\in \Omega(D_1)$, we have $v^g \in \Omega(D_2)$.
Thus, we have
$$ \langle v^g, v^g \rangle_{S^\vee} = \langle w, w\rangle_{S^\vee}$$
for some $w\in \Omega(D_2)$.
However, since $g \in \hbf \subseteq O(\NS(X))$, we have
$$\langle v^g, v^g \rangle_{S^\vee} = \langle v, v \rangle_{S^\vee}$$ and readily deduce that
$$ \langle v, v \rangle_{S^\vee} = \langle w, w\rangle_{S^\vee}.$$
Hence, we infer that the hypothesis
$$D_1 \;\,\text{and} \,\; D_2 \; \, \text{are congruent}$$
implies that
$$ \{ \langle u , u\rangle_{S^\vee} \mid u\in \Omega(D_1) \} =\{ \langle u , u\rangle_{S^\vee} \mid u\in \Omega(D_2) \} . $$
that is, making the assumption that chambers $D_1$, $D_2$ are congruents implies that the respective sets of squares of the elements inducing theirs walls are equal.
Taking the contrapositive, we deduce that if the respective set of squares of elements of $\Omega(D_1)$ and of $\Omega(D_2)$ do not coincide, then
$$D_1 \;\,\text{and} \,\; D_2 \; \, \text{cannot be congruent.}$$
At the code level, if you have to test a chamber $D_1$ against each chamber in a list LIST_REPS_CONG_CLASSES, there are two equivalent possibilities: We refine this initial list of chambers by keeping only chambers having the same number of walls as $D_1$ but also having a set of squares of elements inducing walls that is equal to the set of squares of elements inducing walls of $D_1$.
That is, we define
TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK=[qq for qq in LIST_REPS_CONG_CLASSES if len(qq[3])==len(TEST_CHAMBER[3]) and set([(www[1]*GramMatSinv*transpose(www[1]))[0,0] for www in qq[3]]) == set([(qqq[1]*GramMatSinv*transpose(qqq[1]))[0,0] for qqq in TEST_CHAMBER[3]])]and then test $D_1$ for congruency against each chamber in this list.
The name
TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK
of this list will often be abbreviated as
T_B_T_S_N_W_W_S_C
from now and until the end of this section. Note that the above-mentioned check on squares can also be implemented by adding an if control structure at the beginning of CongCheckerOriginal, the resulting procedure is CongChecker: In this case, the computation of T_B_T_S_N_W_W_S_C is not necessary. The sets of squares of elements inducing walls of $D_1$ and $D_2$ are tested for equality in CongChecker. In case this test returns that the sets of squares are not equal, then $D_1$ and $D_2$ cannot be congruent. Thus, CongChecker immediately returns False. That is, the function CongChecker directly outputs that $D_1$ and $D_2$ are not congruent. In fact, the two chambers are not tested for congruency at all, thus avoiding a waste of time and resources! Otherwise, if the two sets of squares coincide, then CongChecker tests the two chambers against each other for congruency.
In the framework of our example of a chamber $D$ which has to be tested against $80231$ other chambers, we now see that following Professor Shimada’s approach to the letter would have led us
to waste time and resources.
Indeed, we see that we neither have to test $D$ again 80231 chambers, nor have to test it against $60287$ chambers. We go back to our Sage console and compute the above mentioned list
TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK=[qq for qq in LIST_REPS_CONG_CLASSES if len(qq[3])==len(TEST_CHAMBER[3]) and set([(www[1]*GramMatSinv*transpose(www[1]))[0,0] for www in qq[3]]) == set([(qqq[1]*GramMatSinv*transpose(qqq[1]))[0,0] for qqq in TEST_CHAMBER[3]])]and obtain :

In fact, we see that only $23$ congruence tests are needed. Executing the 80208 tests would be a huge waste of time and resources.
Hence, using basic logic and rules of inference enabled us to rigorously show, on a concrete example, that if we followed the approach stated by Prof. Shimada in his $2013$ article,
that $99,97 \%$ of the congruence tests
which would then have to be performed,
are in fact superfluous…
Let’s see how long it takes to perform the so-called 80231 congruence if we take into account the two above-mentioned criterions (number of walls, sets of squares). Define
test_code_CongCheckerOriginal_1 = """
TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK=[qq for qq in LIST_REPS_CONG_CLASSES if len(qq[3])==len(TEST_CHAMBER[3]) and set([(www[1]*GramMatSinv*transpose(www[1]))[0,0] for www in qq[3]]) == set([(qqq[1]*GramMatSinv*transpose(qqq[1]))[0,0] for qqq in TEST_CHAMBER[3]])]
CONG_TEST_RESULTS = []
for qqq in TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK :
CONG_TEST_RESULTS.append(CongCheckerOriginal([q[1] for q in TEST_CHAMBER[3]],[q[1] for q in qqq[3]],qqq[0]))
"""We perform and time the whole operation three times, successively.
times_CongCheckerOriginal_1 = timeit.repeat(stmt = test_code_CongCheckerOriginal_1 ,globals=globals(),number=1,repeat=3) 
We then consider the average time :
mean(times_CongCheckerOriginal_1)
We thus see that testing $D$ for congruence against the $80231$ representatives only took us $6.57$ seconds instead of the 2800 seconds needed when using Prof. Shimada’s approach.
Again, note that only $23$ tests had to be performed. In fact, by timing the computation time of the set TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK, we can see that computing this set takes approx six seconds, and hence is the reason behind the 6.57 total average computation time for testing $D$ against the representatives of chambers. Performing the $23$ congruence tests, in terms of computation times, is almost negligible.
As indicated earlier, there is another way to implement the check related to the sets of squares of elements inducing wall : The procedure CongChecker is obtained by adding an if control sequence at the beginning of CongCheckerOriginal in order to perform this check, so that the computation of TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK is then not necessary since the check on sets of squares is performed chamber by chamber, and the execution of a congruence test is performed only when the sets of squares of walls of both chambers coincide. Define
test_code_CongChecker = """
CONG_TEST_RESULTS = []
for qqq in TO_BE_TESTED_SAME_NBR_WALLS :
CONG_TEST_RESULTS.append(CongChecker([q[1] for q in TEST_CHAMBER[3]],[q[1] for q in qqq[3]],qqq[0]))
"""
As before, we perform the experiment three times consecutively. We measure the total time needed for each execution
times_CongChecker = timeit.repeat(stmt = test_code_CongChecker ,globals=globals(),number=1,repeat=3) and take the average time :
mean(times_CongChecker)
We hence see that the time needed to test $D$ for congruency against the $80231$ representatives of congruence classes has been
reduced to $6.36$ seconds!
Note that the two options regarding the implementation of the check on sets of squares both lead to approximately the same results in terms of computation times.
The fact that here the check on the sets of squares is incorporated within CongChecker makes is particularly suited for parallel deployment, as we will soon see.
We now explain how to perform this experiment with parallel deployment of congruence testing with Pool. Define
def CongChecker_demo_pool(q) :
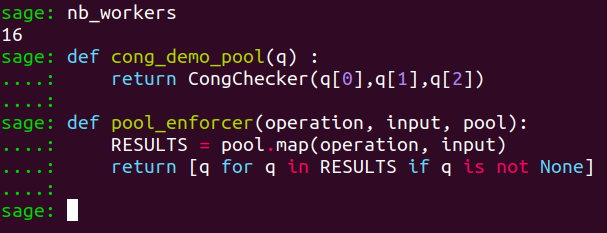
return CongChecker(q[0],q[1],q[2])We define a function pool_enforcer whose purpose consists in mobilizing Pool to split the input data involved during congruence testing and perform the congruence testing operation over various worker processes. Since we loaded init_emb at the beginning of our experiment, the number of worker processes in the pool of processes has been set to one-half the number of logical cores of your CPU.
We take into account all the improvements introduced in this section, and start by taking the list
TO_BE_TESTED_SAME_NBR_WALLS=[qq for qq in LIST_REPS_CONG_CLASSES if len(qq[3])==len(TEST_CHAMBER[3])] as the list containing the chambers against which the chamber $D$ is going to be tested for congruency, since we will use CongChecker which integrates the check for sets of squares.
We organize the list used as input data for Pool as a list of tuples of three elements. For each chamber $D^\prime$ against which $D$ has to be tested, we define a tuple
$$(\Omega(D), \Omega(D^\prime), w_{D^\prime})$$
consisting of the set of walls of $D$, the set of walls of $D^\prime$, and the Weyl vector $w_{D^\prime}$ of $D^\prime$.
We thus use the list
[([q[1] for q in TEST_CHAMBER[3]],[qq[1] for qq in ff[3]],ff[0]) for ff in TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK]as the input data list. Define
test_code_pool = """
CONG_TEST_RESULTS = pool_enforcer(CongChecker_demo_pool,[([q[1] for q in TEST_CHAMBER[3]],[qq[1] for qq in ff[3]],ff[0]) for ff in TO_BE_TESTED_SAME_NBR_WALLS],processes_pool)
"""def pool_enforcer(operation, input, pool):
RESULTS = pool.map(operation, input)
return [q for q in RESULTS if q is not None]We re-define processes_pool again so that our worker processes in the pool of processes are able to execute cong_pool_demo
processes_pool = Pool(nb_workers)We thus test $D$ for congruence against the known representatives of chambers and deploy congruence testing in parallel. We will repeat and time this experiment $5$ consecutive times with timeit.repeat and consider take the average time:
mean(timeit.repeat(stmt = test_code_pool,globals=globals(),number=1,repeat=5))
We obtain that $D$ can be tested for congruency against the $80231$ known representatives
in only $2.18$ seconds!
We now do the same thing but use T_B_T_S_N_W_W_S_C to form the input data list this time, so that we use
[([q[1] for q in TEST_CHAMBER[3]],[qq[1] for qq in ff[3]],ff[0]) for ff in TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK]as input data list and use CongCheckerOriginal instead of CongChecker. Define
def CongCheckerOriginal_demo_pool(q) :
return CongChecker(q[0],q[1],q[2])
processes_pool = Pool(nb_workers)and
test_code_pool = """
TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK=[qq for qq in LIST_REPS_CONG_CLASSES if len(qq[3])==len(TEST_CHAMBER[3]) and set([(www[1]*GramMatSinv*transpose(www[1]))[0,0] for www in qq[3]]) == set([(qqq[1]*GramMatSinv*transpose(qqq[1]))[0,0] for qqq in TEST_CHAMBER[3]])]
CONG_TEST_RESULTS = pool_enforcer(CongCheckerOriginal_demo_pool,[([q[1] for q in TEST_CHAMBER[3]],[qq[1] for qq in ff[3]],ff[0]) for ff in TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK],processes_pool)
"""We execute and measure the time needed to execute this experiment, repeat the operation a total of five times, and take the average execution time :
mean(timeit.repeat(stmt = test_code_pool,globals=globals(),number=1,repeat=5)) 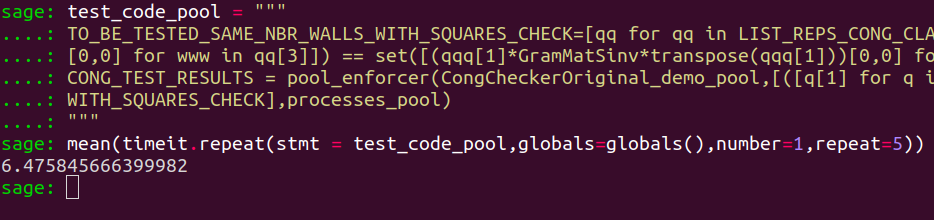
This time, we see that deploying CongCheckerOld in parallel did not bring any noticeable improvement. Why ?
First, note that we had to compute
TO_BE_TESTED_SAME_NBR_WALLS_WITH_SQUARES_CHECK=[qq for qq in LIST_REPS_CONG_CLASSES if len(qq[3])==len(TEST_CHAMBER[3]) and set([(www[1]*GramMatSinv*transpose(www[1]))[0,0] for www in qq[3]]) == set([(qqq[1]*GramMatSinv*transpose(qqq[1]))[0,0] for qqq in TEST_CHAMBER[3]])]This operation, alone, takes approximately six seconds.
Next, the input data list, formed by taking tuples containing data of chambers in T_B_T_S_N_W_W_S_C contains the same number of elements as this list, that is, $23$ elements. It makes no sense and can be counterproductive, to parallelize the execution of a function with an input data list of such a ridiculously small cardinality, especially when a large number of workers, $16$ in our case, are mobilized.
The list T_B_T_S_N_W_W_S_C s obtained by keeping from the list of known representatives only the chambers having the same number of walls as $D$ and for which the set of squares of elements inducing their walls coincides with the set of squares of elements inducing the walls of $D$. By using CongChecker, which integrates the check for the condition on sets of squares, we can in some way distribute the burden of performing the check for this condition over all the workers !
That’s why the computation time is reduced to $2.18$ seconds when parallel deployment of CongChecker is used, instead of the $6.47$ seconds needed with the other approach. The latter, as we recall, requires computing the T_B_T_S_N_W_W_S_C list first (approx. 6 seconds) and then deploying CongCheckerOriginal in parallel over very small input data list, hence in a 100% counterproductive way.
