In his article published in February 2022, Kwangwoo Lee studies the automorphism groups of $K3$ surfaces with Picard number $2$. This publication gives us another opportunity to demonstrate the flexibility and efficiency of our computer-based algorithmic approach to the study of $K3$ surfaces : We will show that applying the Poolized Borcherds’ method instantly leads us to Kwangwoo Lee’s results, with full automation.
We will also show how to use brute force to obtain an initial primitive embedding of the Néron-Severi group of a $K3$ surface into an ambient lattice (see the ambient lattices table).
NB : Finding an initial primitive embedding should not be an obstruction to the use of Borcherds’ method. We never had any issue finding an embedding of the Néron-Severi group of any the surfaces we studied. It is true that we sometimes had to show perseverance to succeed, but in the end, finding an initial primitive embedding has never been an obstacle.
In the section 4.3 of his article, Kwangwoo Lee established that the automorphism group of the $K3$ surface $X$ with Néron-Severi group $S=\NS(X)$ isomorphic to the integral lattice with Gram matrix $$G_S= \begin{bmatrix} 2 & n \\ n & 2 \end{bmatrix}$$ with $n>3$ is generated by
$$ \sigma = \begin{bmatrix} 1 & 0 \\ n & -1 \end{bmatrix} \quad \quad\text{and}\quad \quad \tau = \begin{bmatrix} -1 & n \\ 0 & 1 \end{bmatrix}. $$
Note that we applied a transpose to the matrices provided by Kwangwoo Lee because we use the convention that matrices $M\in O(\NS(X))$ satisfy $$ M G_S M^t = G_S$$ instead of the convention $$ M^t G_S M = G_S$$ which is used by K. Lee in his article.
Let’s start with the case where $n=4$, which has been studied by Joachim Wehler in his 1988 article, that is, the $K3$ surface with $S=\NS(X)$ isomorphic to the integral lattice with Gram matrix $$G_S= \begin{bmatrix} 2 & 4 \\ 4 & 2 \end{bmatrix}$$ with respect to a fixed basis.
Note that there are no $(-2)$-curves on this surface, thus finding an initial ample class will not be a problem. We pick $[100,50]$ as our “ample” class.
Next, we need a primitive embedding $$\iota : S \hookrightarrow \LL = U \oplus E_{8}(-1).$$
We start with a vector $v_1 \in \LL$ having square $2$. For example, we can take $$ v_1 = [1, 1, 0, 0, 0, 0, 0, 0, 0, 0].$$ We then have to find an element $v_2 \in \LL$ such that $v_1$ and $v_2$ have intersection matrix $G_S$ and such that the map $$[x_1 ,x_2 ] \in S \longmapsto x_1 v_1 + x_2 v_2 \in \LL$$ gives a primitive embedding of $S$ into $\LL$.
We seize this opportunity to demonstrate how to proceed using brute force. This technique can be enforced iteratively and generalized to find primitive embeddings for situations in which the $K3$ under study has a bigger Picard number.
We randomly generate vectors of $\LL$ until a suitable one has been found :
Define
GramMatL = load('GramMatL_10.sobj')
LL = IntegralLattice(GramMatL)
v1 = vector([1, 1, 0, 0, 0, 0, 0, 0, 0, 0])
TARGET = Matrix([[2,4],[4,2]])and use the following few lines of code :
while True :
vect_rand = LL.random_element()
MTX = Matrix([v1,vect_rand])*GramMatL*transpose(Matrix([v1,vect_rand]))
if MTX == TARGET and LL.is_primitive(LL.sublattice([v1,vect_rand])) :
break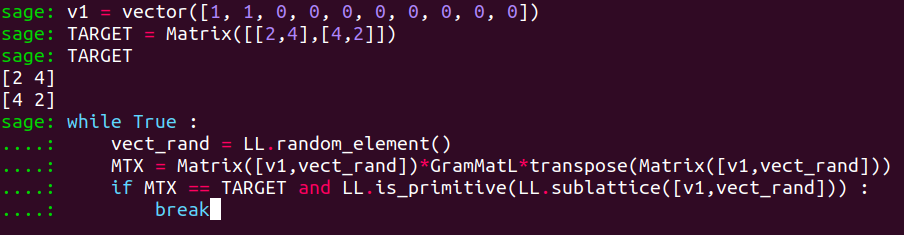
You will quickly obtain a suitable randomly generated vector matching all our requirements.
For example, we obtained :

We thus set
v2 = copy(vect_rand)and define an INPUT_DATA list as follows :
INPUT_DATA = [TARGET,[v1,v2],Matrix([100,50])]
We are now ready to load borcherds_direct.
Just one remark before we proceed further : If you take a look at the code snippet above with the while Loop, you will notice that we make use of Sage’s sublattice and is_primitive functions.
Note that sublattice may return an exception. For example, if it happens that the randomly generated vector vect_rand is a multiple of v1 then Sage will indeed return an exception whenever the command
LL.sublattice([v1,vect_rand])is executed. This behavior, which should be expected, will however break our while Loop.
Two solutions to this issue :
- As we already mentioned numerous times, you can (and should) get rid of Sage if you implement your own version of the Borcherds’ method. Juste take Sage’s source code, and use it to create your own functions. Thus, there are “handcrafted” alternatives to Sage’s sublattice function.
- You can also use Python’s solutions to handle exceptions. Here is a basic example :
while True :
vec_rand = LL.random_element()
MTX = Matrix([v1,vec_rand])*GramMatL*transpose(Matrix([v1,vec_rand]))
try :
BRUTE_PRIM_BOOL = LL.is_primitive(LL.sublattice([v1,vec_rand]))
except :
vec_rand = LL.random_element()
MTX = Matrix([v1,vec_rand])*GramMatL*transpose(Matrix([v1,vec_rand]))
try :
BRUTE_PRIM_BOOL = LL.is_primitive(LL.sublattice([v1,vec_rand]))
except :
vec_rand = LL.random_element()
MTX = Matrix([v1,vec_rand])*GramMatL*transpose(Matrix([v1,vec_rand]))
BRUTE_PRIM_BOOL = LL.is_primitive(LL.sublattice([v1,vec_rand]))
if MTX == TARGET and BRUTE_PRIM_BOOL :
break
Unless you are really unlucky, this code snippet should be enough to deal with a possible exception returned by the sublattice function.
We now return to our study and launch borcherds_direct :
load('borcherds_direct.sage')The program starts

and does not need more than a few seconds to output a generating set of $\aut(X)$.

We see that we thus instantly retrieved the results mentioned in K. Lee’s article : The automorphism group of the $K3$ surface under study is indeed generated by
$$ \sigma = \begin{bmatrix} 1 & 0 \\ 4 & -1 \end{bmatrix} \quad \quad\text{and}\quad \quad \tau = \begin{bmatrix} -1 & 4 \\ 0 & 1 \end{bmatrix}. $$
Let’s give a try to this computation for another value of $n$, say $n=16$, i.e., when $S=\NSX$ has Gram matrix
$$G_S= \begin{bmatrix} 2 & 16 \\ 16 & 2 \end{bmatrix}$$
with respect to a fixed basis. As before, we take
$$v_1 = [1,1,0,0,0,0,0,0,0,0].$$
and set
v1 = vector([1, 1, 0, 0, 0, 0, 0, 0, 0, 0])
TARGET = Matrix([[2,16],[16,2]])We use the above mentioned code snippet to obtain another suitable embedding vector.
After no more than 10 seconds, we obtained

and thus set
v2 = copy(vec_rand)
INPUT_DATA = [TARGET,[v1,v2],Matrix([100,50])]We then load borcherds_direct
load('borcherds_direct.sage')and readily see that we have an issue with the “ample class”.

The program indicates that we can either proceed by using another ample class, or execute emb_updater2. We enforce the KISS principle :
Keep it simple, Keep it stupid
Since there are no $(-2)$-curves on the surface under study, ampleness is a notion which makes no sense for classes of positive self-intersection. All such classes are ample !
We thus follows the path of less resistance and randomly pick another “ample” class.
Let’s use $[555000,5000]$ as our new ample class.
Perhaps a bit overkill, but it should do the job. We set
INPUT_DATA[2] = Matrix([555000,5000])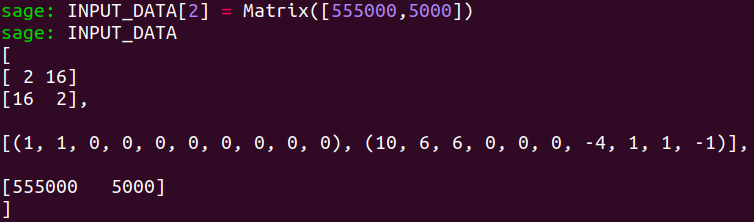
and launch borcherds_direct again.
load('borcherds_direct.sage')This time the program manages to obtain a suitable embedding and automatically launches the Borcherds’ method. After less than two minutes of execution, we obtain :

That is, the automorphism group of the $K3$ under study is generated by
$$ \sigma = \begin{bmatrix} 1 & 0 \\ 16 & -1 \end{bmatrix} \quad \quad\text{and}\quad \quad \tau = \begin{bmatrix} -1 & 16 \\ 0 & 1 \end{bmatrix} $$ exactly as indicated in Kwangwoo Lee’s article.
Let’s study the fundamental domain of the action of $\aut(X)$ onto $\nps$ returned by the Borcherds’ method. Load our fundamentalizer program.
load('fundamentalizer.sage')
As we have already seen during the study of the $K3$ surface from Joachim Wehler’s 1988 article, we expect to obtain that the Hilbert basis produced by fundamentalizer will not bring anything interesting to the table and simply span $\NS(X)$ since there are no $(-2)$-curves on this surface.
This is indeed the case :

