NB : All the data files and programs involved in this section are located in the folder ThesisProgramsJune on the review server
Computation times mentioned in this section are outdated.
From the perspective of the public release of the code, we are currently working on minor optimizations at the code level that enabled us to obtain exciting improvements. The resulting updated Poolized Borcherds’ method can run the example mentioned below in 58 minutes, all by itself, i.e., without assistance from PFB / APFB.
Three fully automated and functional versions of the Borcherds’ method arise from our PhD thesis :
- In terms of structure, the classical Borcherds’ method is very close to Professor Shimada’s 2013 approach to the Borcherds’ method.
- The Poolized Borcherds’ method is a modernized version of the classical Borcherds’ method: We enforced process-based parallelism to deploy the internal procedures of the Borcherds’ method in parallel, e.g., Congruence testing.
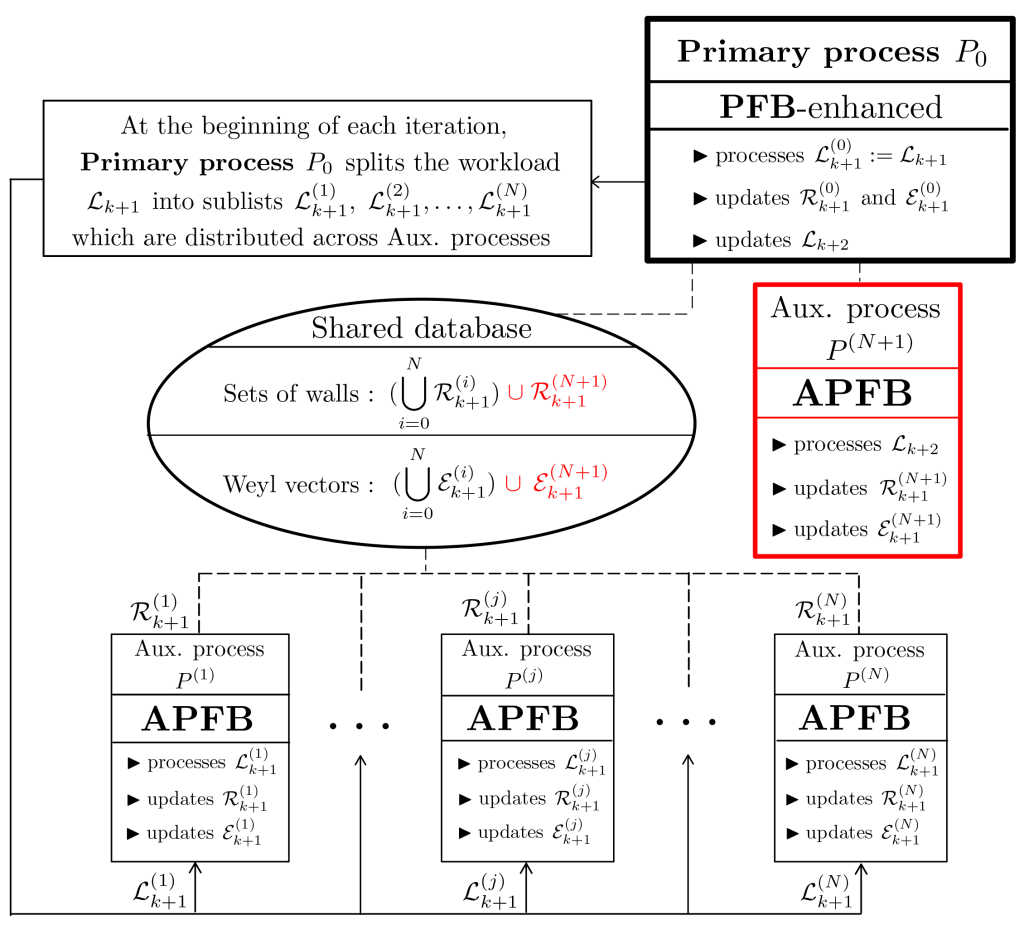
- We pushed our efforts to parallelize the Borcherds’ method even further using the PFB and APFB processes introduced in section 1.11.2 of our thesis, in which we have shown that the burdens of exploring the chamber structure and of computing sets of walls can be distributed over various auxiliary processes deployed in parallel. These processes are also capable of mobilizing their own worker sub-processes to speed up the execution of their internal procedures. This is an essential first step that should greatly facilitate further developments.
Using parallelism and optimization to achieve considerable reductions in computation times on cases for which the method has to explore and process tens of thousands of chambers is one thing. Obtaining similar results on cases for which there are only a few hundreds or thousands of chambers is another. As we already mentioned on this website, we have examples of cases involving tens of thousands of chambers, for which optimizing the code, redesigning procedures & enforcing parallelism enabled us to reduce greatly (e.g., by 700 !) computation times for congruence testing. We would be liars if we asserted that improvements of this magnitude have been obtained for more modest cases. Still, our strategy is based on the use of PFB & APFB, as follows :
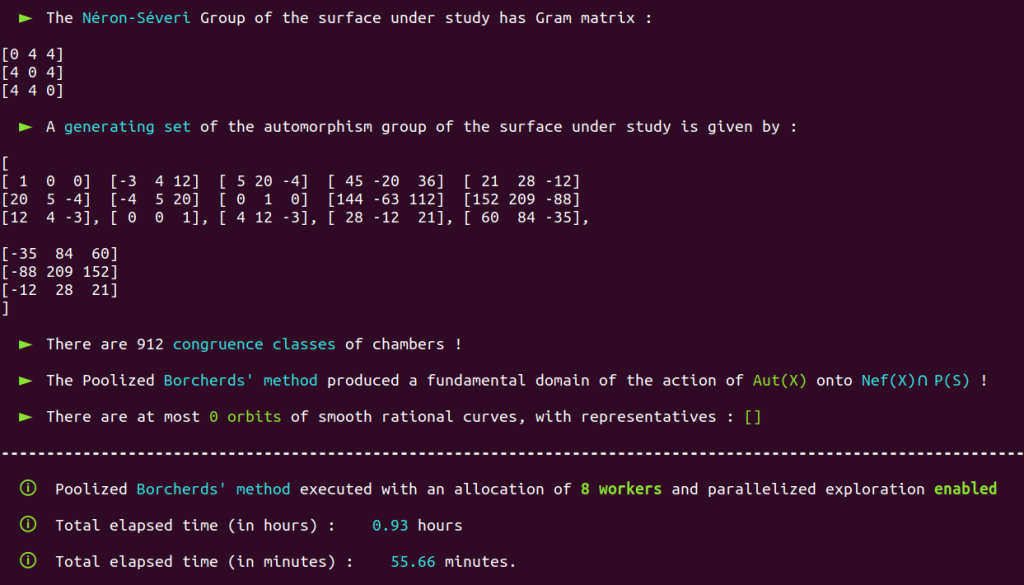
involving various auxiliary processes working to the benefit of a primary process (see section 1.11.2 of our thesis) enabled us to obtain impressive results on cases for which a relatively small number of chambers have to be explored and processed. Consider the $K3$ surface $X$ with Néron-Severi group $S=\NS(X)$ isomorphic to the integral lattice with Gram matrix $$G_S = \begin{bmatrix} 0 & 4 & 4 \\ 4 & 0 & 4 \\ 4 & 4 & 0 \end{bmatrix}$$Using a brute-force flavored approach (see Part One of our study of Kwangoo Lee’s 2022 article), we can quickly obtain that a primitve embedding $$[x_1 ,x_2 ,x_3] \in S \longmapsto x_1 v_1 + x_2 v_2 + x_3 v_3 \in \LL$$ of this lattice into $ \LL = U\oplus E_8(-1)$ is given by the vectors $$v_1 = [ 1, 6, 0, 1, 1, 0, 1, -1, 1, 0 ], \qquad v_2 = [3, 14, 1, 0, 0, -2, 2, -2, 3, -1]$$ and $$v_3 = [1, 3, -1, -1, -2, -3, -1, -1, 0, -1]$$
Using the Poolized Borcherds’ method with an allocation of eight workers for the deployment of the method’s internal procedures with process-based parallelism, computing a generating set of $\aut(X)$ took us 94 minutes. On the same machine, using the PFB-enhanced Poolized Borcherds’ method with an allocation of eight workers and the support of four auxiliary APFB processes, each capable of mobilizing their own eight dedicated worker processes with Pool, computing a generating set of $\aut(X)$ took us 55 minutes.
| Computation of $\aut(X)$ with the Poolized Borcherds’ method, Pool of 8 worker processes | 94 minutes |
| Computation of $\aut(X)$ with the PFB-enhanced Poolized Borcherds’ method, Pool of 8 worker processes Additional assistance of four auxiliary AFPB processes, each capable of mobilizing its own pool of 8 worker processes. | 55 minutes |
Note that further reduced computation times can be obtained by disabling the recovery mode, i.e., disabling the real-time saves of various data files. These saves are done to ensure that computations can be restarted from the point they stopped in case of a power outage, for example. Soon after working on this webpage, we decided that the better course of action consisted in disabling recovery saves by default. The user can activate these saves by setting RECOVERY_BOOL = True before executing the method.