On this page, we explain how to determine whether applying the Borcherds’ method to your complex algebraic $K3$ surface will enable you to obtain a generating set of $\text{Aut}(X)$, according to the logical structure which can be exhibited from Professor Shimada’s 2013 article.
More details regarding this matter can be found in section 1.6 of our thesis.
Contrary to common belief, the Borcherds’ method scope of application is thus quite large… and that’s an understatement.
We divide our study into two parts :
- What conditions should be satisfied for the Borcherds’ method to return a generating set of the automorphism group of the $K3$ surface under study?
- The program ker_checker.
What conditions should be satisfied by $X$ for the Borcherds’ method
to return a generating set of $\text{Aut}(X)$ ?
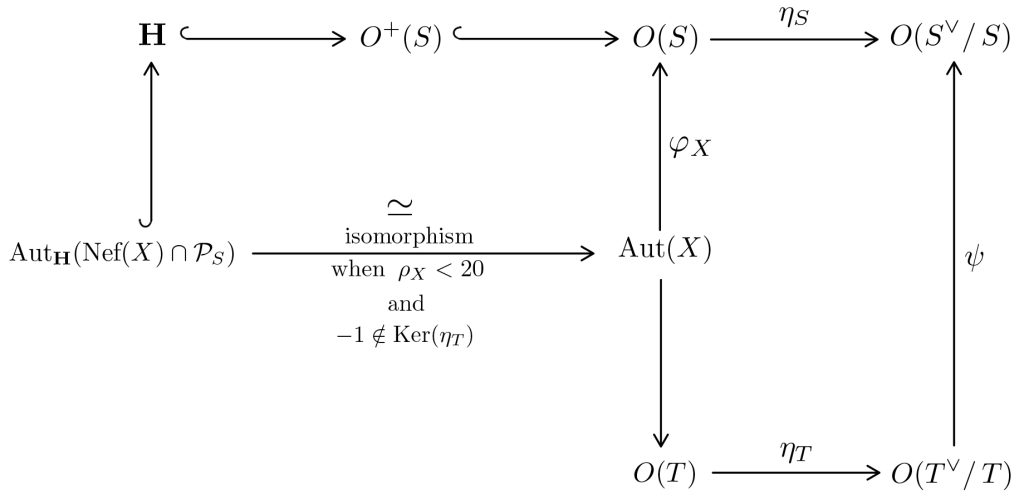
As established by Professor Shimada in his 2013 article, the Borcherds’ method produces a generating set of $\text{Aut}_{\mathbf{H}}(\text{Nef}(X)\cap\mathcal{P}_{S})$ when $X$ is a complex algebraic $K3$ surface for which a suitable initial environment has been setup. The question is then: What condition(s) should be satisfied by $X$ for the Borcherds’ method to return a generating set of $\text{Aut}(X)$?
Let’s quickly review the theoretical background:
Recall that we assume known the data of a primitive embedding $$\iota : S \hookrightarrow \mathbb{L}$$ of $S=\text{NS}(X)$ into a suitable even hyperbolic lattice $\mathbb{L}$, chosen according to the table here.
As indicated in our thesis, we can then
- Define a chamber structure on $\pl$. See section 1.1.2 of our thesis for more details.
- From this chamber structure, we obtain a chamber structure on $\ps$ called the induced chamber structure. Take a look at section 1.2 of our thesis for more details.
- We recall that the $\ps$-chamber structure contains a natural chamber-substructure covering $\nps$. See page 113 in section 1.7 for more details.
Denote by $T$ the transcendental lattice of $X$. Remember that $T$ is defined as the orthogonal complement of $S$ in $$H^{2}(X,\mathbb{Z})\simeq U^{3}\oplus E_{8}(-1)\oplus E_{8}(-1).$$
As indicated in the section 1.6 of our thesis, we can exhibit from Shimada’s 2013 article a logical structure leading to the isomorphism $$\text{Aut}(X)\simeq \text{Aut}_{\mathbf{H}}(\text{Nef}(X)\cap\mathcal{P}_{S})$$ whenever the condition $$-1 \notin \text{Ker}(\eta_T)$$ holds.
Fine. The next question in line is thus :
How can we check whether $-1 \notin \text{Ker}(\eta_T)$ holds ?
Assume that $-1\in\text{Ker}(\eta_{T})$ holds. That is, assume that $-\id \in \ker(\eta_T)$ holds, where $\id$ denotes the $(22-\rho)\times (22-\rho)$-sized identity matrix and where we also recall that $\rho = \text{rank}(S)$.
The matrix transformation $- \text{Id} \in O(T)$ then acts as the identity element of $O(T^{\vee}/\,T)$ by the natural morphism $$\eta_{T} : O(T) \longrightarrow O(T^{\vee}/\,T).$$
It is then clear that $-\text{Id}$ preserves each generator of the discriminant group $T^{\vee}/\,T$.
This can only happen if $- \text{Id}$ preserves
each generator of $T^{\vee}$ modulo $T$
Denote by $$\{b_i \}_{1\leq i \leq 22 -\rho}$$ a possibly non-minimal set of generators of $T^{\vee}$.
We see that the condition in bold implies that
$$-b_{i}-b_{i}\in\mathbb{Z}^{22-\rho} $$
then must hold for $ 1 \leq i\leq 22 – \rho.$
That is, for each $b_i$, we have $$-b_i = b_i + t$$ for some $t \in T$. Since $T$ is an integral lattice of rank $22-\rho$, we have $T\simeq \ZZ^{22-\rho}$.
We thus see how we arrived at the above $-2 b_i \in \ZZ^{22-\rho}$ condition.
Keeping in mind that a possibly non-minimal set of generators of $T^\vee$ can be obtained by taking the set of column vectors of $G_{T}^{-1}$, the above condition on the $b_i$ then amounts to $$-G_{T}^{-1}-G_{T}^{-1}\in \text{GL}_{22-\rho}(\mathbb{Z}),$$ where $G_{T}$ denotes a Gram matrix of the transcendental lattice $T$.
We thus established the following implication :
$$ -\id \in \ker(\eta_T) \Longrightarrow 2G_{T}^{-1} \in \text{GL}_{22-\rho}(\ZZ).$$ Taking the contrapositive of this implication, we obtain
$$
2G_{T}^{-1}\notin \text{GL}_{22-\rho}(\mathbb{Z})\Longrightarrow-\text{Id}\notin\text{Ker}(\eta_{T}).$$
We now have a concrete condition that can be tested without too much effort, thanks to computers :
If $2G_{T}^{-1}$ has a least one rational coefficient, then $$-\text{Id}\notin\text{Ker}(\eta_{T})$$ holds, thus enabling us to assert that the Borcherds method produces a generating set of $\text{Aut}(X)$.
One obstacle remains in front of us : We have to compute a Gram matrix of $T$.
Fortunately, we can easily deal with this obstacle without having to break a sweat when $\,\rho_X \leq 17$.
Since the lattices $$\mathbb{L} = U\oplus E_{8}(-1)$$ and $$\mathbb{L} = U\oplus E_{8}(-1) \oplus E_{8}(-1)$$ are sublattices of the $K3$ lattice $$H^{2}(X,\mathbb{Z})\simeq U^{3}\oplus E_{8}(-1)^{2},$$
any embedding of $S$ into $\mathbb{L}$ can be extended to an embedding of $S$ into the $K3$ lattice in a natural way for surfaces having picard number stricty smaller than $18$.
Since we assume that an embedding of $\text{NS}(X)$ into either $U\oplus E_{8}(-1)$ or $ U\oplus E_{8}(-1)^2$ has been obtained when $\rho_X \leq 17$, we see that computing $G_T$ will not be a problem for such surfaces.
In case the surface under study is such that $\rho_X = 18$ or $19$, obtaining an embedding of $S$ into the $K3$ lattice from the data of an embedding of $S$ into $$\LL = U\oplus E_{8}(-1)\oplus E_{8}(-1)\oplus E_{8}(-1),$$ which is the ambient lattices which should be used for such surfaces, is not guaranteed. This matter will have to be investigated on a case-by-case basis.
The ker_checker program
For complex algebraic $K3$ surfaces with Picard number $\rho_X \leq 17$, obtaining an embedding of $S=\NS(X)$ into $H^2(X,\ZZ)$ is the job of the ker_checker program. The latter will then compute a Gram matrix $G_T$ of the transcendental lattice $T$ and test whether the condition $$2G_{T}^{-1}\notin \text{GL}_{22-\rho}(\mathbb{Z})$$ holds. Let’s show how things work on the computer. As before, we assume that the $K3$ surface under study has Néron-Severi group $\text{NS}(X)$ with Gram matrix $$ G_S = \begin{bmatrix} 4 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & -2 \end{bmatrix}$$ with respect to a fixed basis. We also assume that you are either connected to the demo server or that you downloaded our programs bundle, extracted the folder ThesisPrograms and opened a Sage console pointing to it. Load the associated input data :
INPUT_DATA = load('INPUT_DATA/DIAG_PICARD_THREE/INPUT_DATA_DIAG_PICARD_THREE_case_2.sobj')
and load init_emb to define the initial environment, as explained here :
load('init_emb.sage')Load ker_checker :
load('ker_checker.sage')The program then immediately provides an answer regarding whether the Borcherds’ method will return a generating set of $\text{Aut}(X)$ if applied to the $K3$ surface $X$ under study:

Let’s work on an example for which we know that $-1\in \ker(\eta_T)$, so that ker_checker should this time return a negative answer. In the section $9$ of his 2013 article, article in which, as we mentioned in our thesis, can be found all the pieces of the puzzle, Prof Shimada suggests that $-1\in \ker(\eta_T)$ when the surface under study is the $K3$ surface with $S=\NS(X)$ isomorphic to the lattice with Gram matrix
$$\begin{bmatrix} 0 & 1 & 0 \\ 1 & -2 & 0 \\ 0 & 0 & -2 \end{bmatrix}$$
so that there is no guarantee that the Borcherds’ method will return a generating set of $\aut(X)$ if executed to study this surface. We use ker_checker to determine whether $-1 \in \ker(\eta_T)$ holds. Enter the command:
INPUT_DATA=load('INPUT_DATA/SHIMADA_SURFACES_PICARD_THREE/INPUT_DATA_SHIMADA_SURFACES_PICARD_THREE_case_1.sobj')to load the input data related to Shimada’s surface. You can either directly load borcherds_direct.sage or proceed step-by-step by launching init_emb and then launching ker_checker. Note that the borcherds_direct program is designed to automatically execute the Borcherds’ method if all conditions to do so are fulfilled and calls for ker_checker to determine whether the condition $-1 \notin \ker(\eta_T)$ holds.
Load borcherds_direct :
load('borcherds_direct.sage')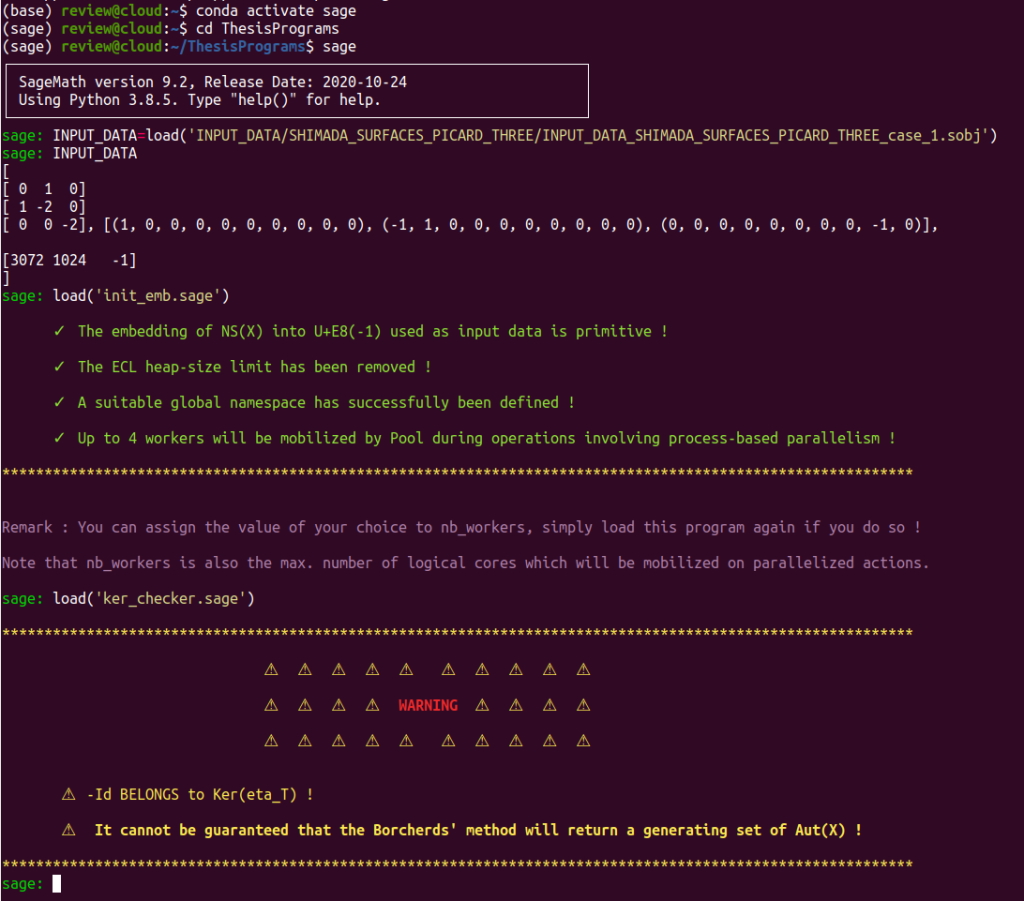
The program borcherds_direct stops because ker_checker determined that $\id \in \ker(\eta_T)$…
Thus confirming Prof. Shimada’s writings.
