Embedding Update

April 21: In addition to emb_updater2, another modernization
to our implementation emb_updater of Prof. Shimada’s 2013 embedding
update procedure will be released as emb_updater3

We now explain how to update an embedding $\iota : S \hookrightarrow \mathbb{L}$ in order to obtain the nondegeneracy of an initial $\mathcal{P}_{\mathbb{L}}$-chamber $\mathcal{D}_0$ in such a way that the $\mathcal{P}_{S}$-chamber

$$D_0 = \DD_0 \cap \ps$$

thus induced is contained in $\text{Nef}(X)\cap\mathcal{P}_S$.

Fundamental concepts & Notations

We start by quickly reviewing the background regarding the fundamental concepts and notations.

We denote by $\mathcal{P}_{\mathbb{L}}$ the positive cone of the ambient lattice $\mathbb{L}$ into which $S=\NS(X)$ is assumed to be primitively embedded by an embedding $$\iota : S\hookrightarrow \mathbb{L}.$$

We define a chamber structure on $\mathcal{P}_{\mathbb{L}}$. Elements of this chamber structure are called $\mathbb{P}_{\mathbb{L}}$-chambers. See sections 1.1.2 and 1.2 of our thesis for more details. A $\mathcal{P}_{\mathbb{L}}$-chamber $\mathcal{D}$ is said to be $\iota(S)$-nondegenerate whenever the intersection $$\mathcal{D}\cap\mathcal{P}_S$$ has non-empty interior. When this is the case, the chamber $\mathcal{D}$ induces a $\mathcal{P}_S$-chamber $$D=\mathcal{D}\cap \mathcal{P}_S$$ on the positive cone $\mathcal{P}_S$ of $S$. This is how a chamber structure on $\mathcal{P}_S$ is obtained.

The elements of this chamber structure are called $\ps$-chambers.

Understanding why we need to provide the Borcherds’ method with an initial $\mathcal{P}_S$-chamber contained in $\text{Nef}(X)\cap \mathcal{P}_S$.

The Borcherds’ method needs a starting point to start exploring and processing the chamber structure over $\text{Nef}(X) \cap \mathcal{P}_S$. That is, the Borcherds’ method needs to be provided with an initial $\mathcal{P}_S$-chamber $D_0$ contained in $\text{Nef}(X) \cap \mathcal{P}_S$.

For each of the three possible even hyperbolic ambient lattices mentioned in this table, a suitable Weyl vector $w_0$ associated with a $\mathcal{P}_{\mathbb{L}}$-chamber $\mathcal{D}_0$, as indicated in Prof. Shimada’s 2013 article.

Assuming that the $\pl$-chamber $\DD_0$ with Weyl vector $w_0$ cannot be asserted as nondegenerate, and that an ample class $a_0$ such that $a_0 \notin \text{Int}(\DD_0 \cap \ps)$ is known, we explain how to proceed in order to obtain an updated embedding $$\iota_\text{upd} : S \hookrightarrow \mathbb{L}$$ from the data of $a_0, w_0$ and of the initial embedding $\iota : S \hookrightarrow \LL $, in such a way that $$\iota_\text{upd}(a_0)\in\text{Int}(\mathcal{D}_0 \cap \ps)$$ so that it can be asserted that $\DD_0$ induces a $\mathcal{P}_S$-chamber $$D_0 = \mathcal{D}\cap\mathcal{P}_S$$ contained in $\text{Nef}(X) \cap \mathcal{P}_S$, thus providing the Borcherds’ method with an initial $\ps$-chamber $D_0$ from which can begin the exploration of the $\mathcal{P}_S$-chamber structure over $\text{Nef}(X) \cap \mathcal{P}_S$.

Obtaining such a chamber is essential: Indeed, if you provide the Borcherds’ method with an initial $\mathcal{P}_S$-chamber is not contained in $\text{Nef}(X) \cap \mathcal{P}_S$, then the method will forever be stuck outside of the $\text{Nef}(X) \cap \mathcal{P}_S$ area of study…

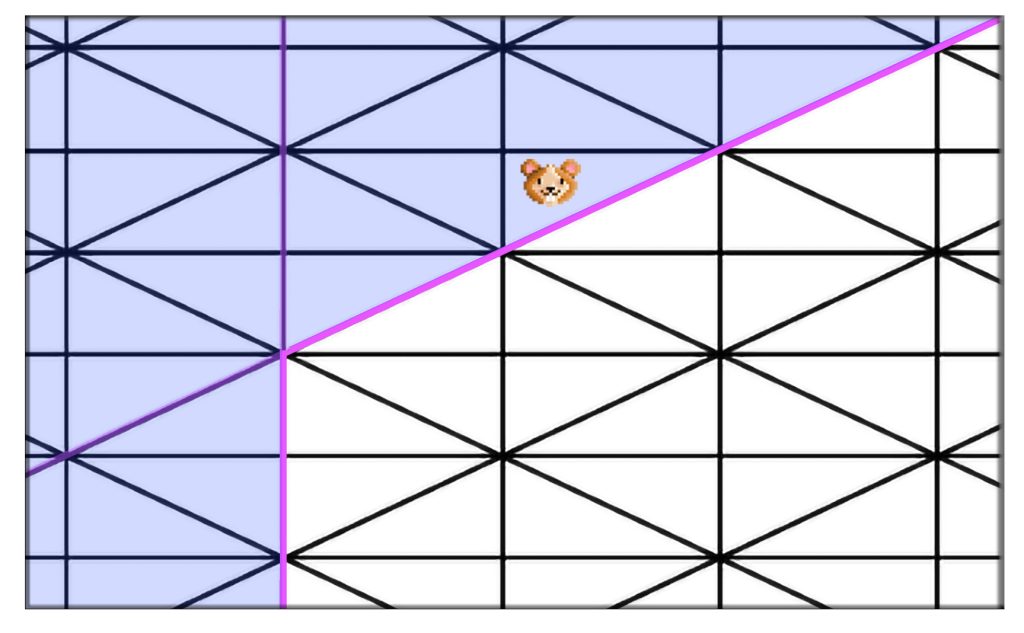
Borcherds’ method (Hamster) stuck outside of $\text{Nef}(X) \cap \mathcal{P}_S$, whose complement has been colored with transparent blue. Two $(-2)$-walls, in purple, prevent the Borcherds’ method from entering the chamber structure over $\text{Nef}(X) \cap \mathcal{P}_S$.

You don’t want to be stuck like the Hamster pictured above. Indeed, let’s consider that this Hamster represents Borcherds’ method. It is forever stuck outside of the chamber structure over $\text{Nef}(X) \cap \mathcal{P}_S$ : Recall that $\text{Nef}(X) \cap \mathcal{P}_S$ is bound by $(-2)$-walls, and that a core principle of the Borcherds’ method is that such walls cannot be crossed. That is, the method is not allowed to compute the Weyl vector of a $\mathcal{P}_S$-chamber $D^\prime$ adjacent to a $\mathcal{P}_S$-chamber $D$ contained in $\text{Nef}(X) \cap \mathcal{P}_S$ along a $(-2)$-wall, because $D^\prime$ is not contained in $\text{Nef}(X) \cap \mathcal{P}_S$ !

The Borcherds’ method relies on the RatDetect to avoid crossing such adjacencies. As indicated by its name, the procedure RatDetect, from section 1.7.1 of our thesis, detects such walls and enables the Borcherds’ method to avoid crossing these dangerous adjacencies.

Section 1.8 of our thesis contains all the details on the procedures that can be enforced to update an embedding so that a suitable initial chamber is obtained.

In this section, we start by presenting the idea outlined by Professor Shimada to do so in his 2013 article and then introduce our version of Prof. Shimada’s procedures, which solves all the problems and limitations of Shimada’s original ideal.

Embedding update procedure
A battle fought at the level of the $\mathcal{P}_{\mathbb{L}}$-chamber structure.

Updating an embedding is a battle fought at the level of the $\mathcal{P}_{\mathbb{L}}$-chamber structure.

Indeed, asserting the $\iota(S)$-nondegeneracy of a $\mathcal{P}_{\mathbb{L}}$-chamber can only be done by exhibiting a class $a_0 \in \mathcal{P}_S$ such that $$\iota(a_0) \in \text{Int}(\mathcal{D}_0 \cap \mathcal{P}_S)$$ holds. What are the causes which prevent this condition to be fulfilled ?

This happens when either

  • $\iota(a_0)$ belongs to a wall of $\mathcal{D}_0$, that is, to the boundary of $\DD_0$ or when
  • $\iota(a_0)\notin \text{Int}(\mathcal{D}_0)$

Remark : Note that we always know at least one element contained in the interior of a $\pl$-chamber : By definition, the Weyl vector $w\in \mathbb{L}$ of a $\pl$-chamber $\mathcal{D}$ satisfies $w\in \text{Int}(\DD)$.

Making the additional assumption that $a_0$ is ample enables us to assert than any $\pl$-chamber $\DD$ containing $\iota(a_0)$ in its interior induces a $\ps$-chamber $D_0$ contained in $\text{Nef}(X) \cap \mathcal{P}_S$.

We also assume that $\iota(a_0)$ does not belong to the boundary of $\mathcal{D}_0$, i.e., to we assume that $\iota(a_0) \notin (r)^\perp$ for some element $r\in \LL$ such that $\langle r,r\rangle_{\LL}=-2$ such that $(r)^\perp$ is a wall of $\DD_0$.

This assumption is crucial because all the limitations of Shimada’s original procedure arise from a situation in which $\iota(a_0)$ is “stuck” in a wall of $\mathcal{D}_0$, as we will soon see.

When $\iota(a_0)$ is neither in the interior of $\mathcal{D}_0$ nor stuck into one of its walls then $\iota(a_0)$ is contained in some $\mathcal{P}_{\mathbb{L}}$-chamber $\mathcal{D}\neq \mathcal{D}_0$, as illustrated below :

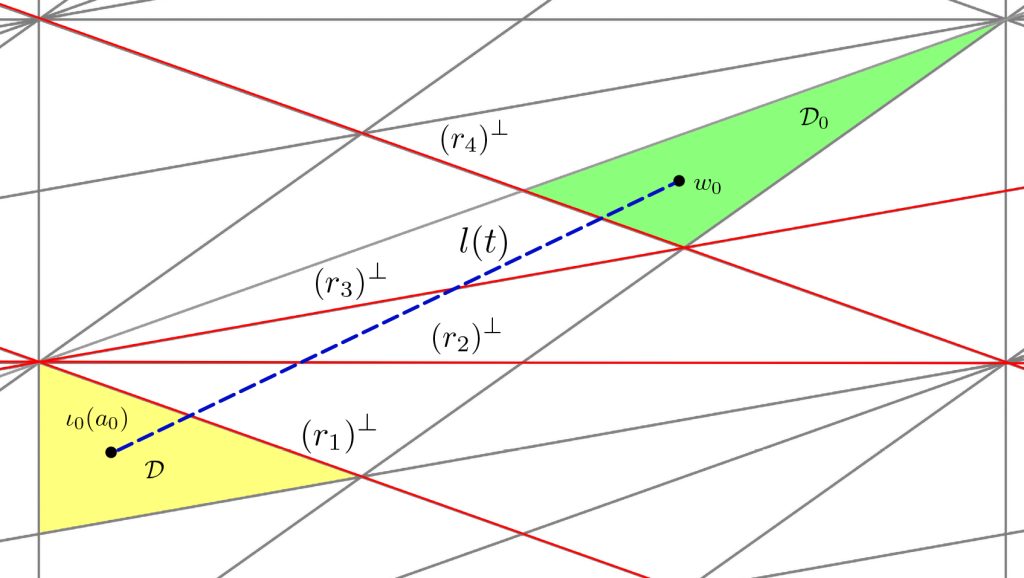
This illustration is a mock-up of what happens at the level of the $\mathcal{P}_{\mathbb{L}}$-chamber structure when $\iota(a_0)\notin \text{Int}(\mathcal{D}_0)$. Unlike all our other chamber structure diagrams, which are based on real pictures of chunks of a $\mathcal{P}_S$-chamber structure from cases in which $S$ has Picard number $3$, this one is 100% made up for illustrative purposes.

Shimada’s idea original idea regarding an embedding update procedure for nondegeneracy consists in enumerating the walls in $\pl$ separating $\iota(a_0)$ from $w_0$, that is, Shimada determines the set

$$ \{ x\in \mathbb{L} \mid \langle \iota(a_0) , x \rangle_{\mathbb{L}} < 0, \; \langle \iota(a_0), x\rangle_{\mathbb{L}} > 0, \, \langle r ,r \rangle_{\mathbb{L}} =-2\}.$$

As displayed on the above figure, we assume that this set is made of $r_1,r_2,r_3,r_4$, each having square $-2$ in $\LL$ are have orthogonal complements defining walls $(r_1)^\perp,\, (r_2)^\perp,\, (r_3)^\perp$ and $(r_4)^\perp$ of the $\pl$-chamber structure.

Shimada’s then applies to the initial embedding $\iota : S \hookrightarrow \mathbb{L}$ a transformation $$\tau : \mathbb{L} \longrightarrow \mathbb{L} $$ obtained as $$\tau=s_{r_{4}}\circ s_{r_{3}}\circ s_{r_{2}}\circ s_{r_{1}} $$ by composition of the reflections $$s_{r_i}:x\longmapsto x+\left\langle x,r_i\right\rangle _{\mathbb{L}}r_i$$ with respect to each wall $\;(r_i)^\perp$ in the hope that the resulting updated embedding $$\tau\circ\iota:S\hookrightarrow\mathbb{L}$$ we be such that $$\left(\tau\circ\iota\right)(a_{0})\in\text{Int}(\mathcal{D}_{0}\cap\mathcal{P}_S)$$ thus ensuring the $(\tau\circ\iota)(S)$-nondegeneracy of $\mathcal{D}_0$.

NB: As soon as an updated embedding has been obtained, you have to re-define the initial environment required to execute the Borcherds’ method in the framework of this new embedding. Everything is 100% automated with our programs.

Shimada’s idea embodies the core mechanics that should be used to update an embedding and obtain nondegeneracy, but the procedure that enforces these mechanics has many flaws. As indicated by Shimada himself, a successful outcome to this procedure may require many attempts. Shimada recommends using another ample class as input data whenever the procedure fails, without any precise explanation.

We identified all the limitations of Prof. Shimada’s original embedding update procedure and built on our findings to produce a modernized embedding update procedure from which the “lottery” aspect has been entirely removed. Our approach is more in line with the spirit of dynamic programming: Instead of applying many reflections to the initial embedding in one go, we proceed step by step.

Section 1.8 of our thesis contains more details and explanations regarding this matter.

Preliminary work & testing nondegeneracy with degentest

We now proceed to the computer-based side of our study, and explain how to update an embedding by studying an example. Load the input data we provide for the study of the $K3$ surface with Néron-Severi group $S$ having Gram matrix $$ G_S = \begin{bmatrix} 4 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & -2 \end{bmatrix} $$ with respect to a fixed basis. That is :

 INPUT_DATA = load('INPUT_DATA/DIAG_PICARD_THREE/INPUT_DATA_DIAG_PICARD_THREE_case_2.sobj')

Load the program init_emb.sage :

load('init_emb.sage')

We already discussed in this section how to determine with ker_checker whether the Borcherds’ method will return a generating set of $\aut(X)$. We have seen that an application of the Borcherds’ method to the surface under study will indeed produce a generating set of $\text{Aut}(X)$. We now focus on the embedding update procedure.

Note that the input data list INPUT_DATA contains a class in $S$:

This class is ample and will play the role of the class $a_0$ from our previous discussion. We provide in section 2.3 of our thesis a technique to determine an initial ample class.

When loaded, the program init_emb automatically assigns the variable amp0 to INPUT_DATA[2], i.e., to the above ample class.

Note that the variable Weyl has been assigned by init_emb to a row matrix element of $\mathbb{L}$

which will play the role of the Weyl vector $w_0$ in our above discussion.

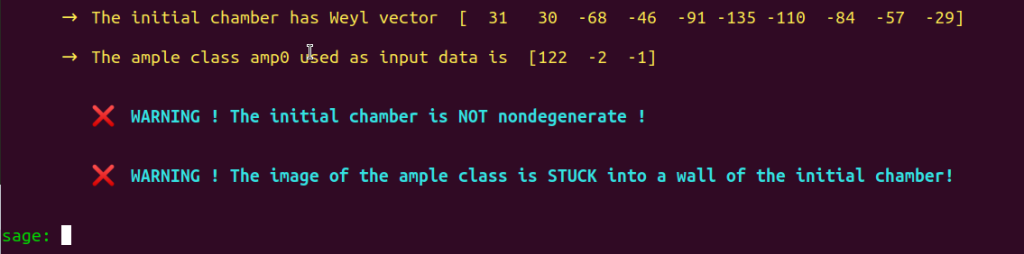
As indicated by Shimada in his 2013 article, this Weyl vector is the Weyl vector of an initial $\mathcal{P}_\mathbb{L}$-chamber $\mathcal{D}_0$. Our program degentest enables you to determine whether the image of this ample class in $\mathbb{L}$ is contained in the interior of $\mathcal{D}_0 \cap \mathcal{P}_S.$

The program degentest will thus determine whether $\mathcal{D}_0$ can be asserted as $\iota(S)$-nondegenerate. Load this program :

load('degentest.sage')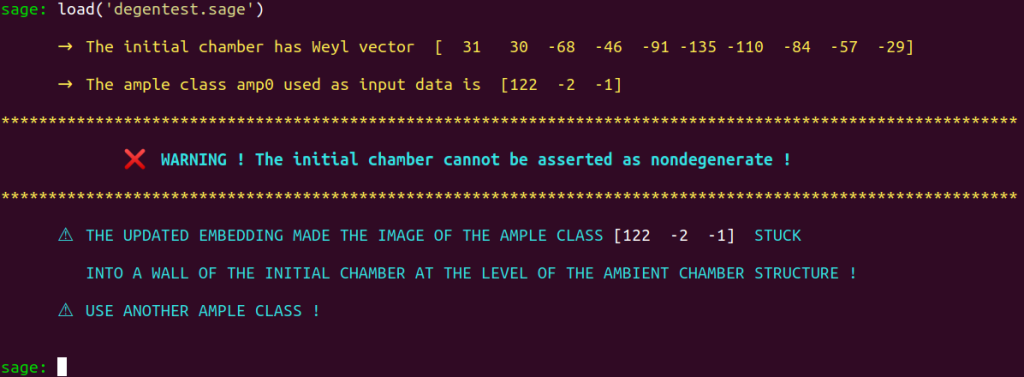
The program degentest determined that the $\pl$-chamber $\DD_0$ cannot be asserted as nondegenerate from the data of the initial embedding $\iota :S \hookrightarrow$ and of the ample class in the global namespace, that is, $\iota(a_0) \notin \text{Int}(\DD_0\cap\ps)$

Other than a visual indication, the output of degentest is consists of two booleans BOOL_DEGEN and BOOL_STUCK.

The value False is assigned to BOOL_DEGEN whenever the nondegeneracy test fails. When the chamber under study can be asserted as nondegenerate, BOOL_TEST will receive the value True.

If the image of the ample class $\iota(a_0)$ used as input data is stuck into a wall of $\mathcal{D}_0$, then BOOL_STUCK will be True. Otherwise, it will be False.

These booleans are checked by the program borcherds_direct.

This program automatically executes all the required checks and launches the Borcherds’ method when all the conditions required to do so are met.

Note that an additional warning is displayed when BOOL_STUCK is true :

To make sure that everything is clear regarding cases in which $\iota(a_0)$ is stuck into a wall of the initial chamber, please take a look at the following figure :

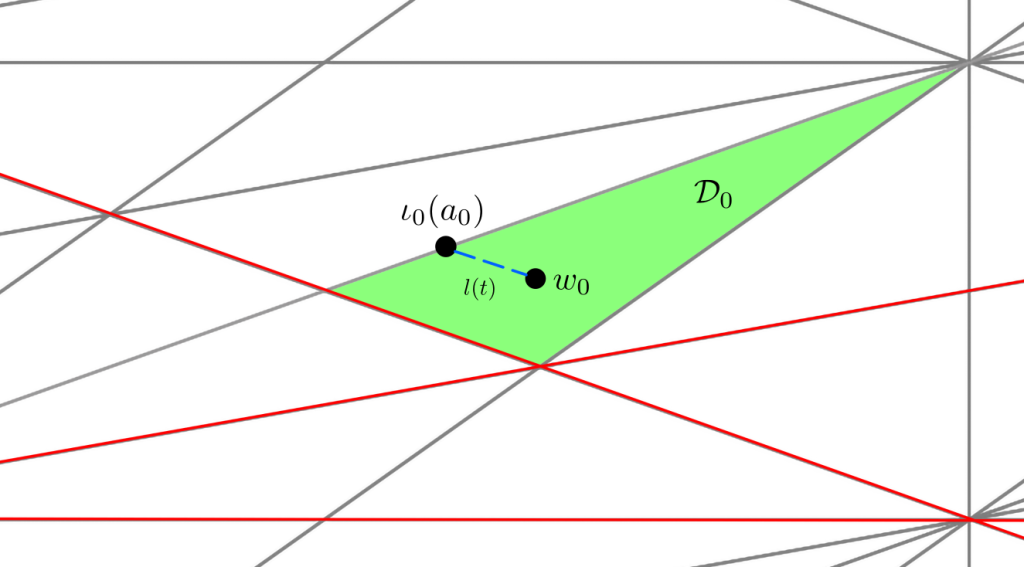
$\iota(a_0)$ is displayed as stuck into a wall of $\DD_0$.

When such a situation occurs, you have no leeway. The mechanics of the embedding update procedure rely on the application of reflections with respect to walls crossing the path between $\iota(a_0)$ and $w_0$. When $\iota(a_0)$ is stuck into a wall of $\DD_0$, there is no wall separating it from $w_0$, except the wall into which it is stuck. Since reflections of the form

$$s_{r_i}:x\longmapsto x+\left\langle x,r_i\right\rangle _{\mathbb{L}}r_i$$ act as the identity on elements $x\in (r_i)^\perp$, you will not be able to do anything to free $\iota(a_0)$ from the wall into which it is stuck. The only thing you can do is either find another primitive embedding or find another ample class. Shimada did not explain why he asked his readers to use another ample class when the procedure outlined in his 2013 article fails. We hope our explanations provide a better understanding of what’s happening behind the scenes.

Regarding the case under study, we see that the program degentest indicates that the initial chamber $\mathcal{D}_0$ cannot be asserted as $\iota(S)$-nondegenerate. That is, the image in $\mathbb{L}$, which can be found under the variable amp0LL, of our ample class $a_0$ is not contained in the interior of $\text{Int}(\mathcal{D_0})$.

We thus have to update our embedding. Since BOOL_STUCK is false, all lights are green to start updating our embedding. We provide two means to do so :

  • The program emb_updater follows the guidelines provided by Shimada in his 2013 article.

This is one of the few sections of our code involving Magma. We do so by using the Sage / Magma interface, which provides a gateway to bring Magma’s features into the world of Python. More precisely, we used Magma in our program ShiChecker (based on an algorithm by Prof. Shimada) to compute the set

$$ \{ x\in \mathbb{L} \mid \langle \iota(a_0) , x \rangle_{\mathbb{L}} < 0, \; \langle \iota(a_0), x\rangle_{\mathbb{L}} > 0, \, \langle r ,r \rangle_{\mathbb{L}} =-2\}$$ of walls in $\pl$ crossed by the path separating $\iota(a_0)$ from $w_0$. The Magma function involved in this computation still displays unmatched performance compared to its Pythonic alternatives. Nevertheless, we also provide a Magma-free, much slower version of emb_updater, which can be found under the emb_updater_MagmaFree.

  • We also provide a modernized version of Shimada’s embedding update procedure, which will enable you to deal with the cases for which emb_updater cannot obtain an embedding under which the nondegeneracy for $\mathcal{D}_0$ can be asserted : emb_updater2.sage

Program emb_updater

Let’s start with emb_updater :

load('emb_updater.sage')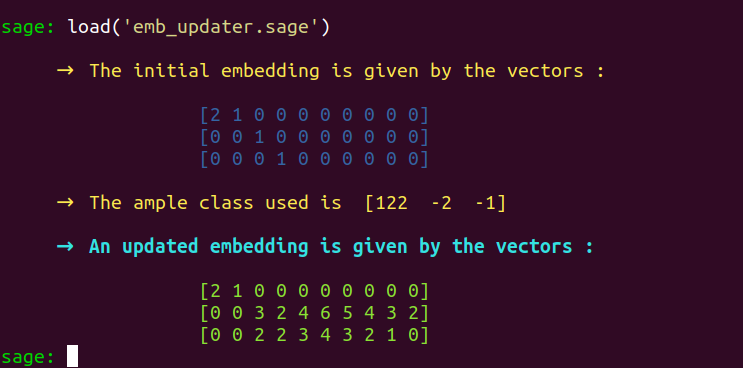

This program produces an updated embedding. You then have to rerun degentest in order to determine whether this embedding is such that $\iota(a_0)\in \text{Int}(\mathcal{D}_0)$. That is, to determine whether $\mathcal{D}_0$ can be asserted as nondegenerate. Note degentest will be automatically executed after the execution of emb_updater if a variable AUTOTEST to which has been assigned the value True can be found in the global namespace before the execution of emb_updater.

Let’s see if the resulting updated embedding suits our needs :

load('degentest.sage')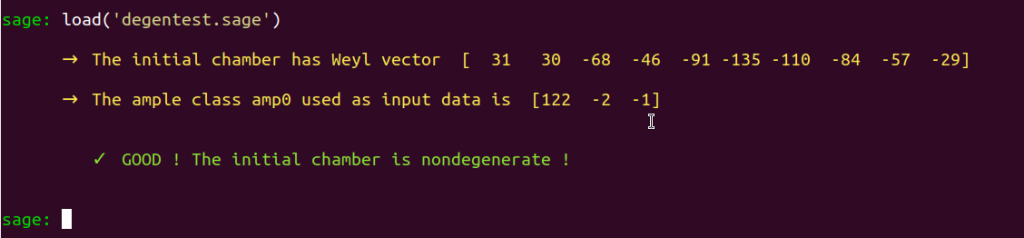

Great ! Do not forget to verify that $-1 \notin \text{ker}(\eta_T)$ holds by running ker_checker. If this condition holds, then you can execute the Borcherds’ method, as explained on this page.

You are now ready to run the Borcherds’ method!

Program emb_updater2

The program emb_updater2 is a modernized version of emb_updater: An updated embedding is computed by proceeding step-by-step: Each wall separating $\iota(a_0)$ from $w_0$ is seen as an obstruction that must be cleared. To do so, the program starts by clearing the closest obstruction to $\iota(a_0)$. It then updates the embedding by applying a single reflection ; the reflection with respect to this obstruction, and then updates the list of obstruction which remain between $\iota(a_0)$ and $w_0$ in the framework of the updated embedding.

That is, instead of applying many transformations in one go to the initial embedding, emb_updater2 proceeds obstruction by obstruction and updates the list of obstructions as soon as the embedding is updated.

This program follows the basic principles of dynamic programming :

  • A system is in an initial state A.
  • An agent takes a decision and makes a move.
  • This move has an impact on the state of the system.
  • The system is now in state B.
  • The agent takes the new parameters of the system into account before making a decision and making its next move.
  • Etc…

The program, therefore, takes the parameters of the new configuration into account before making a decision and making its next move. This is the general idea behind emb_updater2.

We provide more details about this matter in section 1.8.3 of our thesis.

To use emb_updater2 you can proceed exactly as we indicated previously when we provided guidelines for using emb_updater. Let’s launch

load('emb_updater2.sage')

with $S$ defined as a sublattice ok $\LL$ thanks to the updated embedding obtained earlier.

Since the embedding used as input data already enables us to assert nondegenereacy for $\DD_0$, the program emb_updater2 does not detect any obstruction because the embedding used as input data has already been updated and meets all the requirements by providing nondenegeneracy. :

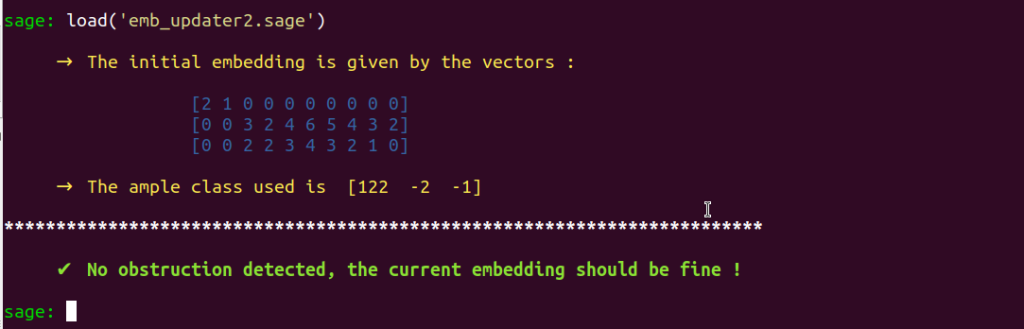
To illustrate the inner workings of this program, we reload the initial embedding specified by the vectors in INPUT_DATA[1] :

load('init_emb.sage');

The program emb_updater2.sage starts its execution and performs as many iterations as needed to remove the obstructions while taking into account the whole new configuration after each update of the embedding :

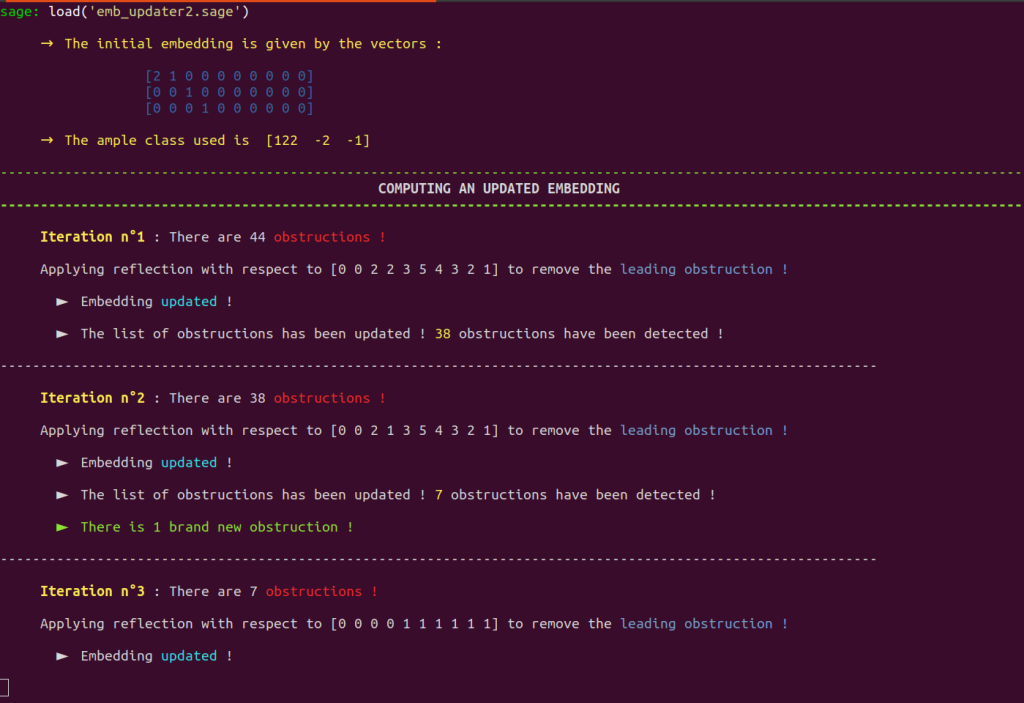
Note that emb_updater2 obtains the same embedding as emb_updater. The same embedding as our implementation emb_updater of Shimada’s original embedding update procedure.

However, emb_updater2 obtained this result by applying only $4$ transformations, while emb_updater mechanics made it apply $44$ transformations to the initial embedding, leading to the same result!

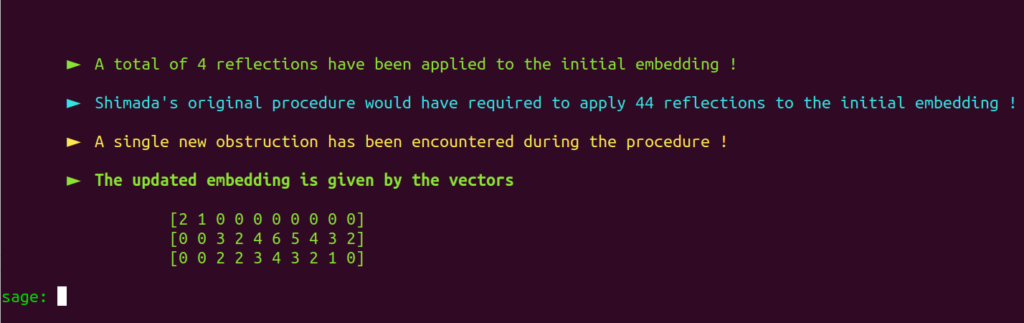
Remember that emb_updater2 will be a valuable resource when emb_updater cannot satisfactorily update an embedding.