- ⚠ Taking the set of walls of $D$ modulo $\text{Aut}_{\mathbf{H}}(D)$ ⚠
- ⚠ The need for an anti-backtracking procedure (obvious, but may be overlooked !) ⚠
Let $D$ be a $\mathcal{P}_S$ chamber. When Borcherds’ method explores the adjacencies along the walls of $D$, three facts should be taken into account; we start with the first two and deal with the third a few paragraphs below.
- The Borcherds’ method is not allowed to explore adjacencies along (-2)-walls because such walls would make the method leave its $\text{Nef}(X)\cap \mathcal{P}_S$ area of study. Identifying such walls is the purpose of the procedure RatDetect.
- In his 2013 article, Prof. Shimada states that the set of walls $\Omega(D)$ should be taken modulo $\text{Aut}_{\mathbf{H}}(D)$ when considering adjacencies along $D$.
We have already dealt with the first point. Regarding the next one, a few remarks: Note that we exclusively studied surfaces with a small Picard number (per the goals defined to complete our doctoral studies). However, we put in place tools with much larger application scope. For all the surfaces we studied, the condition $$\text{Aut}_{\mathbf{H}}(D)=\{1\}$$ has always been satisfied for all chambers explored. Shimada has also reported this phenomenon on the surfaces he studied ten years ago.
Thus, for us, the set of walls $\Omega(D)$ modulo $\text{Aut}_{\mathbf{H}}(D)$ is simply $\Omega(D)$.
However, we always proceeded while having generality in mind. Our programs will thus compute a set of representatives of all the orbits of $\Omega(D)$ under the action of the finite group $\text{Aut}_{\mathbf{H}}(D)$.
You will indeed find a function ORB_FINDER in our code, calling for some GAP stuff, which will take care of this whenever $\text{Aut}_{\mathbf{H}}(D)$ is not trivial.
When $\text{Aut}_{\mathbf{H}}(D)$ is trivial, ORB_FINDER is not used since doing so is unnecessary; as we said, the output would be $\Omega(D)$.
But please be aware that to save space on figures, we neither refer to some procedure OrbFinder (with associated function ORB_FINDER) in figures nor in the thesis.
Let’s talk about this function right now. Providing additional content is also one of the purposes of this website.
If you want to code your version of the Borcherds’ method, and have issues with an ORB_FINDER function, do not worry. Here is the code :
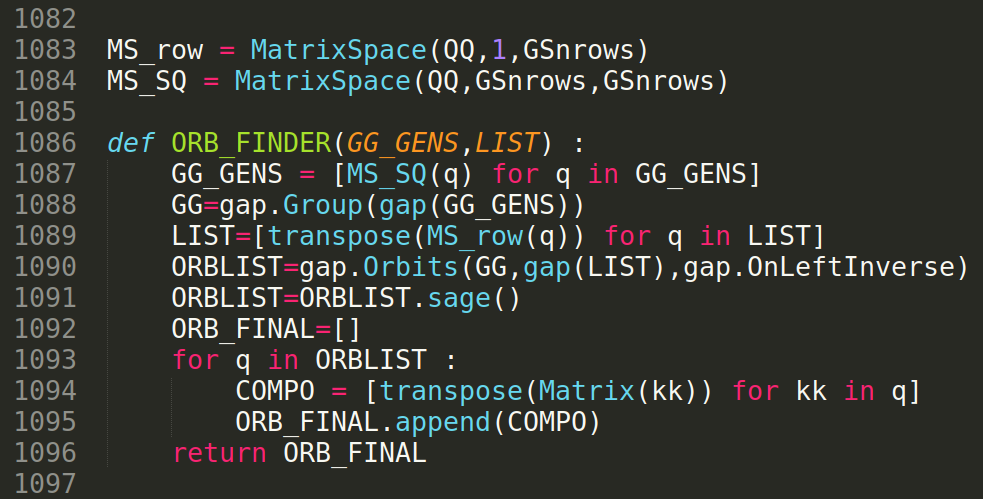
We use the Sage / Gap interface to bring GAP-related stuff into the world of Python.
The input consists of a set GG_GENS of generators of $\text{Aut}_{\mathbf{H}}(D)$, and of the list LIST of walls of $D$. GSnrows is the Picard number of the $K3$ under study, i.e., the number of rows of a Gram matrix of its Néron-Severi.
Anti-backtracking
The third fact which should be taken into account is the following :
- Whenever the Borcherds method explores the adjacencies along with a chamber $D$ of level $k$, it should not consider adjacencies along the walls leading to chambers of level $k-1$.
Indeed, these chambers have already been explored and processed during the previous iterations. Thus, the method also needs an “anti-backtracking” procedure to immediately recognize a wall of a chamber leading to a chamber of a lower level (which can only be the level of the current chamber, decreased by $1$).
The need for an anti-backtracking procedure seemed so obvious to us that you will not find a single mention of such a procedure in the current version of our thesis…
Since its early days, even our most basic, primitive implementation of the method incorporated an anti-backtracking feature.
Since we want to deal will all the aspects of the Borcherds’ method, the next update of the PDF file will contain remarks regarding anti-backtracking.
We will, however, not add a functional block to our figures for such an obvious procedure.
Sets of walls & associated notations
Anyways, we will consider anti-backtracking by updating some notations: Denote by $\Omega(D)$ the set of walls of a $\mathcal{P}_S$-chamber $D$. That is, $\Omega(D)$ is a primitively minimal defining set of $D$. We moreover assume that $D$ is of level $k$.
- We denote by $\overline{\Omega}(D)$ the set of walls of $D$ minus the walls leading to chambers of level $k-1$. That is, $\overline{\Omega}(D)$ can be considered as the set obtained after the application of the anti-backtracking procedure (3 lines of code at most, do not worry) on $\Omega(D)$.
- We then denote by $\overline{\Omega}_{\ast}(D)$ the set obtained after application of RatDetect to each element of $\overline{\Omega}(D)$. That is, the set $\overline{\Omega}_{\ast}(D)$ is the set non (-2)-walls of $D$, taking into account the removal of the walls leading to chambers of level $k-1$.
Keeping track of adjacencies
Also, we recommend that you add to your implementation of the Borcherds’ method a feature to identify chambers that have already been explored (quite prominent, of course !).
You can proceed by creating an adjacency database so that the method can keep track of all adjacencies in real-time. Another possibility consists in using identification by Weyl vectors: As soon as the method computes a Weyl vector, it looks at a list of Weyl vectors of chambers that have already been explored. If the Weyl vector newly obtained belongs to this list, then the associated chamber is not explored since it has already been explored earlier!
For cases with small Picard numbers, computing Weyl vectors is so fast that you can afford to use identification by Weyl vectors. For cases with a significant Picard number, use an adjacency database; it will help you save resources.
We had one issue with the adjacencies database: We used Sage, which enabled us to save time by bringing into the world of Python a HUGE number of useful advanced mathematical functions. There is a small price to pay for all these benefits: We have to deal with Sage objects, and one should always keep in mind that Sage objects containing a lot of data can be huge and slow to save and load.
Since our methods integrate a recovery feature, which regularly saves the data produced in a “recovery” folder, which then enables you to restart a computation from the point at which it was stopped in case of an unexpected event (power outage, computer crash, segmentation error, i.e., the usual events met when you work with computers all day long), saving and updating a huge database of adjacencies is an issue for us.
June 2, remark: The recovery feature is disabled by default. Activation of recovery is controlled with the boolean RECOVERY, e.g., set RECOVERY = True before executing the method to enable regular saving of data files to create an image of the progress of the method.
We used a strategy based on identification by Weyl vector, which spares us from dealing with potentially weighty Sage objects to save regularly. Indeed, doing so could unnecessarily slow down the entire procedure.
