In this 2016 article Automorphisms of surfaces in a class of Wehler surfaces with Picard number $4$, Prof. Baragar studies automorphisms of the Wehler $K3$ surface with Picard number $4$.
The $K3$ surface under study has a Néron-Severi group isomorphic to the integral lattice with Gram matrix
$$J = \begin{bmatrix} 0 & 2 & 2 & 0 \\
2 & 0 & 2 & 1 \\
2 & 2 & 0 & 1 \\
0 & 1 & 1 & -2 \end{bmatrix}$$
with respect to a fixed basis. Before proceeding further, note that Baragar uses the convention that elements $M\in O(\NS(X))$ satisfy $$ M^t J M = J$$ while we use the convention that an elements $M\in O(\NS(X))$ instead satisfy $$M J M^t = J.$$
In what follows, we thus took the transpose of all the matrices involved in Baragar’s article.
In this article, Baragar states that $$ \langle \sigma_1,\sigma_2,\sigma_3,\sigma_4\rangle$$ is a finite index subgroup of $\aut(X)$ and denotes by $\sigma_i^{\ast}$ the action of these automorphisms on the Néron-Severi group of $X$. In terms of matrices, Baragar provides a precise characterization regarding $\sigma_2^\ast$ and $\sigma_3^\ast$ :
$$\sigma_2^{\ast} = \begin{bmatrix} 1 & 0 & 0 & 0 \\
2 & -1 & 2 & 0 \\
0 & 0 & 1 & 0 \\
1 & 0 & 0 & -1
\end{bmatrix},\qquad \sigma_3^{\ast} = S_2 \sigma_2^{\ast} S_2 = \begin{bmatrix} 1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
2 & 2 & -1 & 0 \\
1 & 0 & 0 & -1
\end{bmatrix} $$ where $$S_2 = \begin{bmatrix} 1 & 0 & 0 &0 \\
0 &0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \end{bmatrix}.$$
Regarding $\sigma_1^\ast$ and $\sigma_4^\ast$, Baragar narrows down the range of possibilities as follows :
- Prof. Baragar states that either $\sigma_1^\ast = T_1$ or that $\sigma_1^\ast = S_1 T_1$,
- Prof Baragar states that either $\sigma_4^{\ast} = T_4$ or that $\sigma_4^{\ast} = S_1 \sigma_3^{\ast} T_4$,
where the matrices $T_1, S_1$ and $T_4$ are defined as :
$$ T_1 = \begin{bmatrix} -1 & 2 & 2 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -1 & 1 & 1 & 1 \end{bmatrix} ,\qquad S_1 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & -1\end{bmatrix}$$ and $$ T_4 = \begin{bmatrix} -1 & 8 & 0 & 4 \\
0 & 1 & 0 & 0 \\
-2 & 8 & 1 & 4 \\
0 & 0 & 0 & 1
\end{bmatrix}$$
That is, either $$\sigma_1^\ast = T_1 = \begin{bmatrix} -1 & 2 & 2 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -1 & 1 & 1 & 1 \end{bmatrix} \qquad \text{or} \qquad \sigma_1^\ast =S_1 T_1 = \begin{bmatrix} -1 & 2 & 2 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 1 & -1 \end{bmatrix} $$ and either $$ \sigma_4^{\ast} = T_4 = \begin{bmatrix} -1 & 8 & 0 & 4 \\
0 & 1 & 0 & 0 \\
-2 & 8 & 1 & 4 \\
0 & 0 & 0 & 1 \end{bmatrix} \qquad \text{or} \qquad \sigma_4^{\ast} = S_1 \sigma_3^{\ast} T_4 = \begin{bmatrix} -1 & 8 & 0 & 4 \\
0 & 1 & 0 & 0 \\
0 & 10 & -1 & 4 \\
0 & 0 & 0 & 1\end{bmatrix}$$
We use the Poolized Borcherds method to clarify the situation regarding the automorphism group of Baragar’s Wehler $K3$ surface with Picard number $4$.
Doing so will enable us to obtain a precise answer regarding $ \sigma_1^{\ast} $ and $ \sigma_4^{\ast} $.
As explained here, the preliminary input required consists of a Gram matrix of $\NS(X)$, of vectors that define an embedding of $\NS(X)$ into $\mathbb{L} = U\oplus E_8(-1)$ and of an initial ample class.
If you are currently on the demo server, or if you downloaded our archive containing the folder ThesisPrograms, please open a Sage console and proceed as follows :
INPUT_DATA = load('INPUT_DATA/DEMO/INPUT_DATA_WEHLER_PICARD_FOUR.sobj')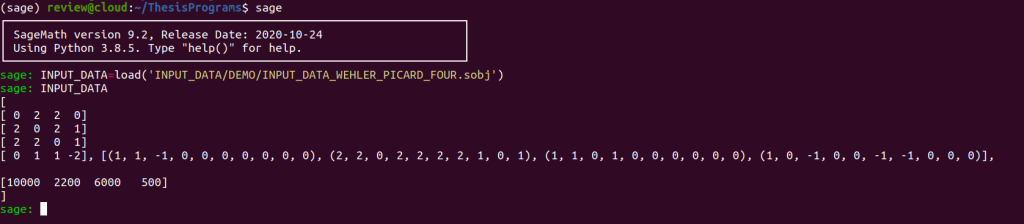
Load init_emb to set up the initial environment for the Borcherds’ method :
load('init_emb.sage')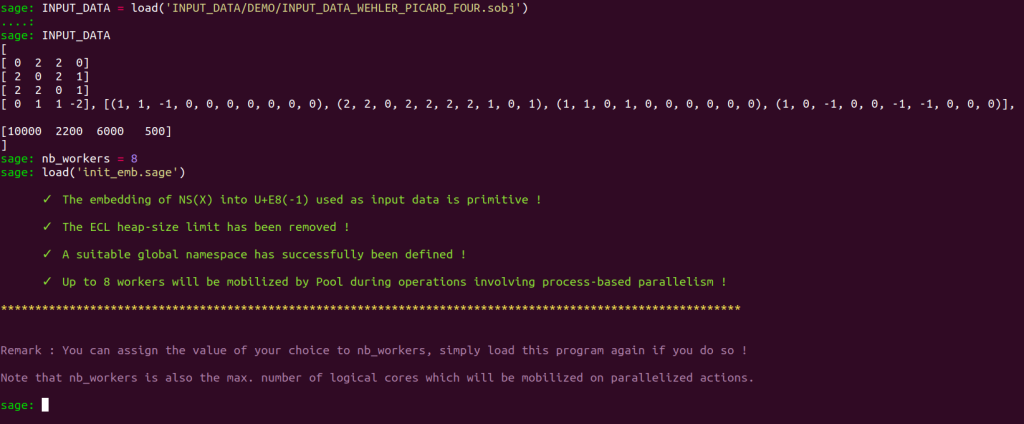
Note that the ample class $[10000,2200,6000,500]$ we provided in input data is ridiculous.
We will find another class with more “realistic” coefficients.
Load proj_mod, and let’s use AmpTester to find another ample class.
Let’s try $[100,22,60,5]$ :
load('proj_mod') ;
AmpTester(Matrix([100,20,60,5]))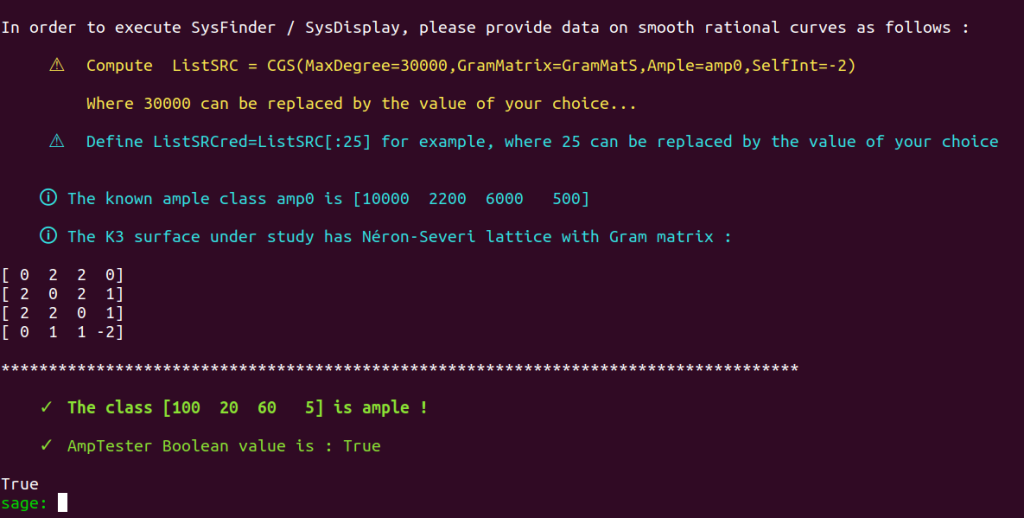
Fine. Let’s define :
INPUT_DATA[2] = Matrix([100,20,60,5])and load init_emb again :
load('init_emb.sage')We are ready to take off.
First, we start by checking whether applying the Borcherds’ method to the $K3$ surface under study will provide a generating set of $\aut(X)$. Load ker_checker :
load('ker_checker.sage')
Great.
The Borcherds method will provide.
Load degentest to determine whether we have in hand a nondegenerate$\mathcal{P}_\mathbb{L}$-chamber inducing a $\mathcal{P}_S$-chamber contained in $\nps$ which can be used as starting point by the method for its exploration of the chamber structure over $\nps$.
load('degentest.sage')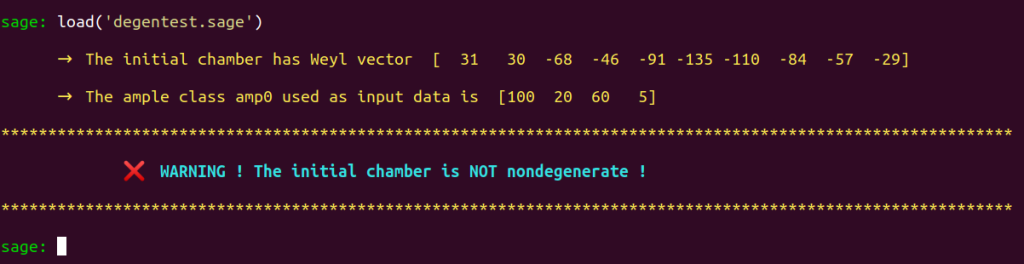
Our initial embedding has to be updated.
To this end, we load our modernized version of Shimada’s embedding update procedure :
load('emb_updater2.sage')The mechanics behind this procedure are explained in section 1.8.3 of our thesis.
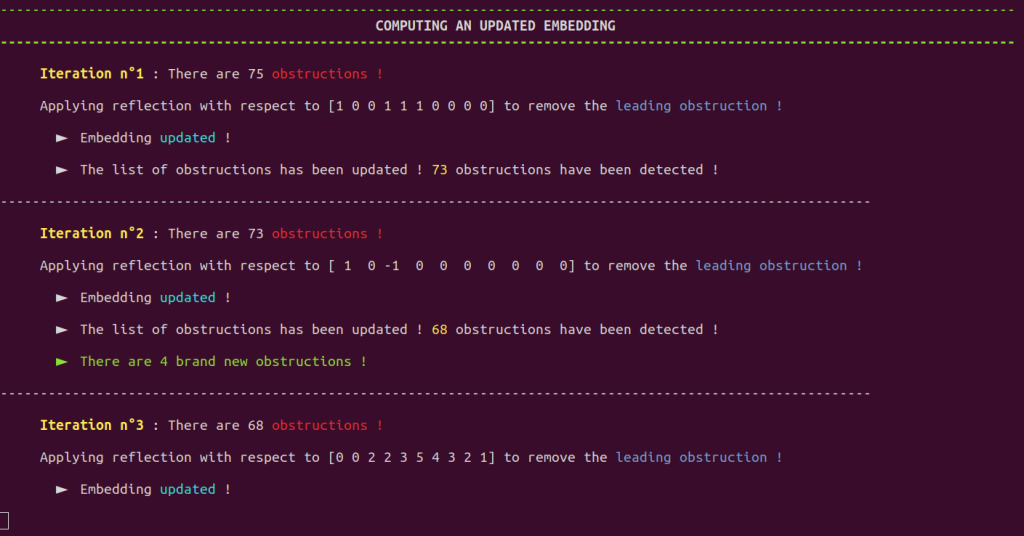
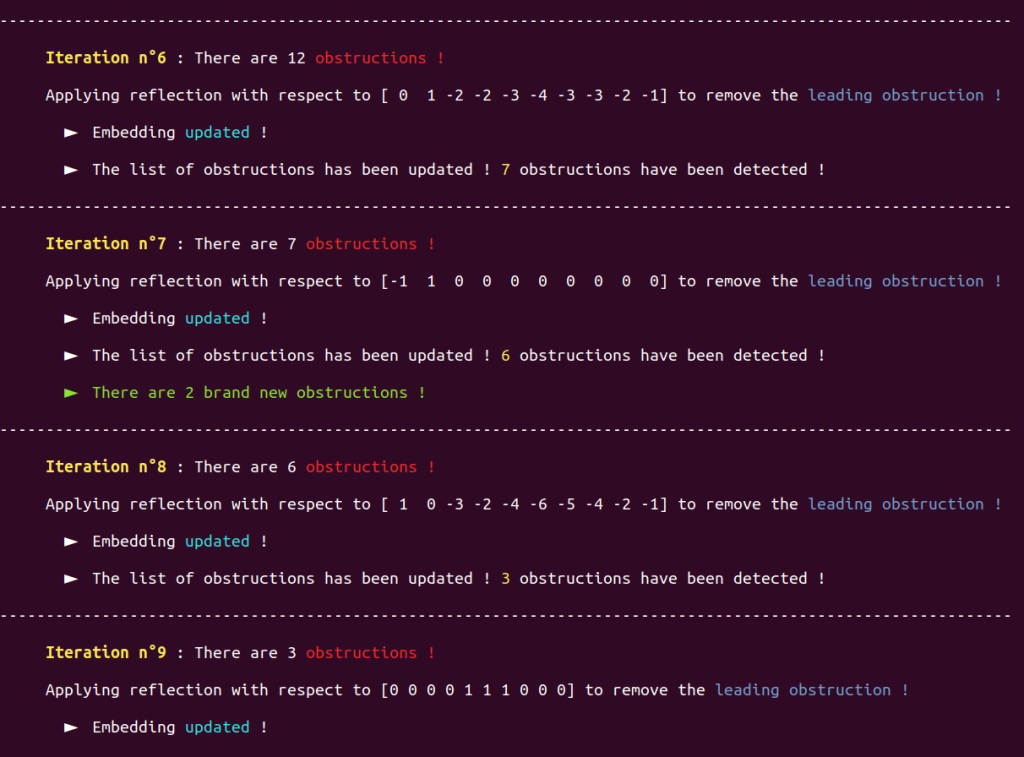
The further the procedure progresses, the fewer obstructions there are (again, please take a look at section 1.8.3 of our thesis for more details) :
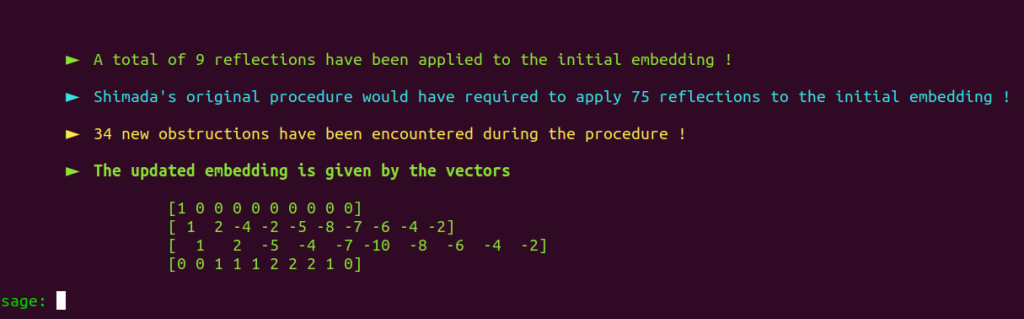
The procedure finally obtains an updated embedding :
Let’s apply degentest again :
load('degentest.sage')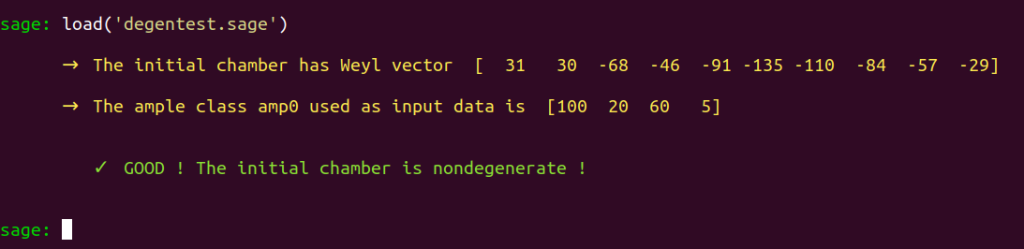
Great! We are ready to launch the Borcherds method!
Assign the strings of your choices for the variables text1 and text2, which will be used to personalize the name of the files produced by the method :
text1 = str('Wehler_picard_4')
text2 = str('Baragar')Since we are running the program on our demo server, we only have $8$ cores at our disposal. Using a Pool of $8$ worker processes will be OK. Set :
nb_workers = 8We then launch the Poolized Borcherds’ method (process-based parallelism with Pool) :
load('borcherds.sage')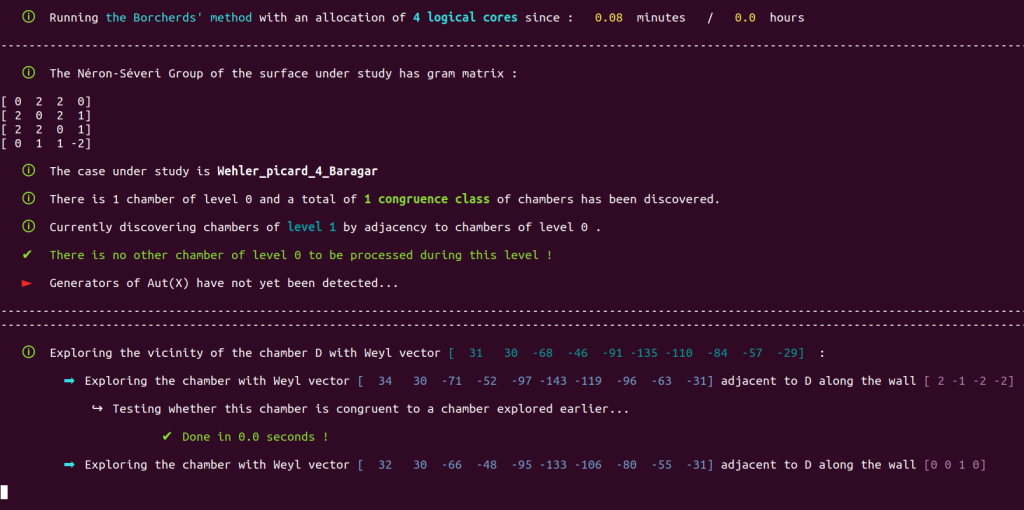
Since we don’t like waiting, we also launched the computation on must faster machine than the demo server, with an allocation of 20 workers. Here is the result :
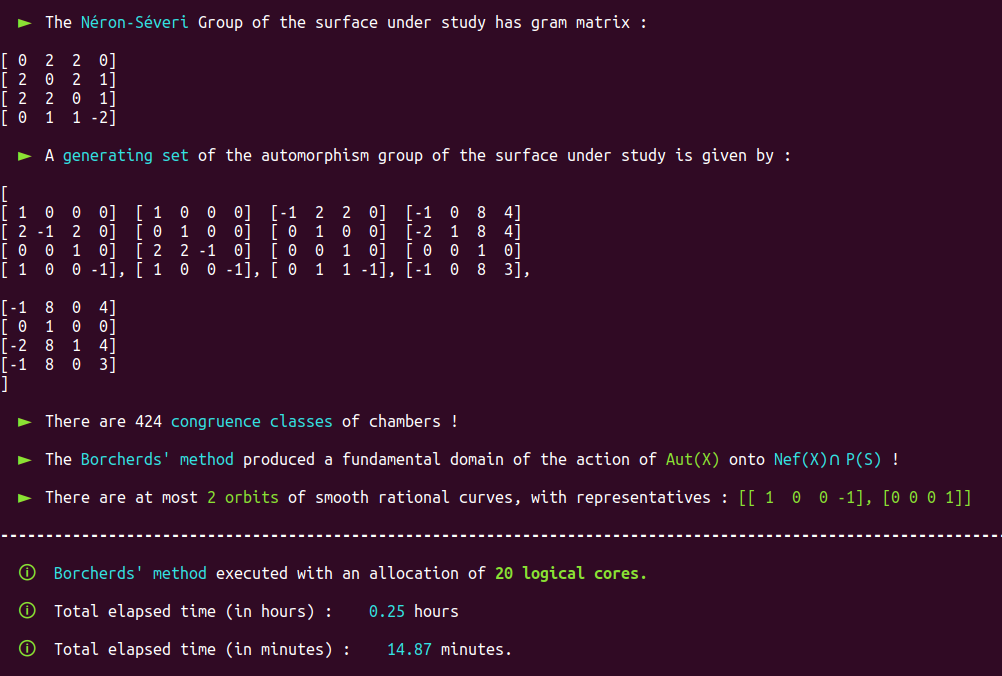
The Borcherds’ method thus returns that a generating set of $\aut(X)$ is given by
$$g_1= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 2 & -1 & 2 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & -1 \end{bmatrix}, \qquad g_2 = \begin{bmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 2 & 2 & -1 & 0 \\ 1 & 0 & 0 & -1 \end{bmatrix}, \qquad g_3 = \begin{bmatrix} -1 & 2 & 2 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & -1 \end{bmatrix} ,$$ $$g_4 = \begin{bmatrix} -1 & 0 & 8 & 4 \\ -2 & 1 & 8 & 4 \\ 0 & 0 & 1 & 0 \\ -1 & 0 & 8 & 3 \end{bmatrix} ,\qquad g_5 = \begin{bmatrix} -1 & 8 & 0 & 4 \\ 0 & 1 & 0 & 0 \\ -2 & 8 & 1 & 4 \\ -1 & 8 & 0 & 3 \end{bmatrix},$$ that the union of the $424$ representatives of congruence classes of chambers is a fundamental domain of the action of $\aut(X)$ onto $\nps$ and that there are at most two orbits of smooth rational curves with representatives $$[1,0,0,-1] \qquad \text{and} \qquad [0,0,0,1].$$
Before focusing on Baragar’s study, let’s apply our program fundamentalizer in the hope that interesting data regarding the above-mentioned fundamental domain can be extracted :
load('fundamentalizer.sage')
The program fundamentalizer will start a thorough analysis of the walls of the chambers forming the fundamental domain to identify its boundary walls.
This analysis will enable fundamentalizer to determine whether a convex cone can be associated with the fundamental domain. The program will return a Hilbert basis of the fundamental domain when this is the case.
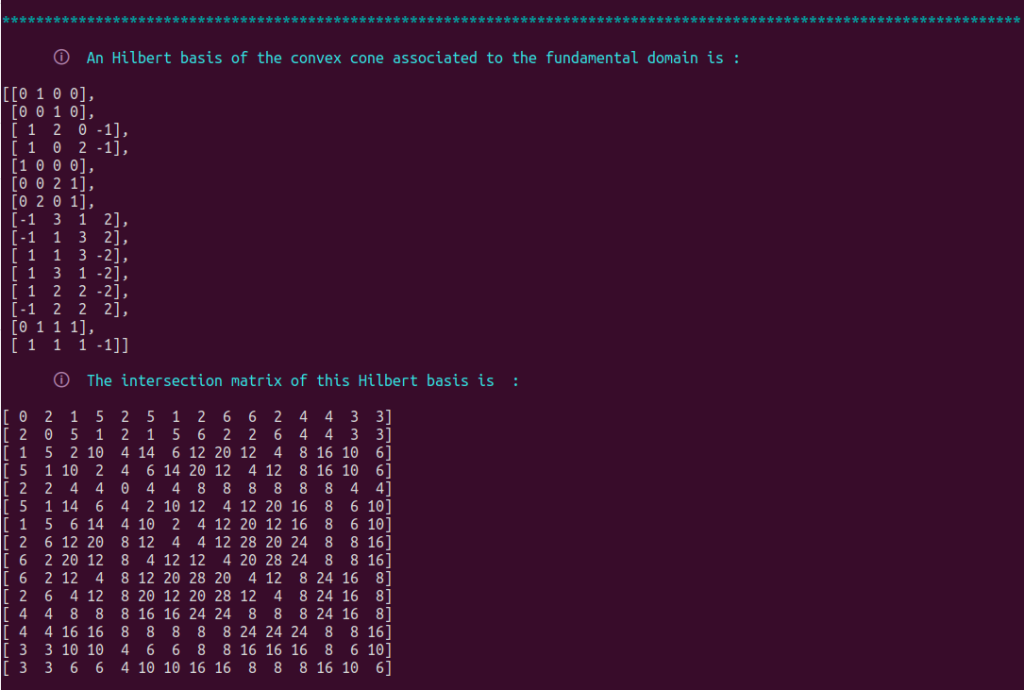
We thus obtain that $$[[0, 1, 0, 0 ], [0, 0, 1, 0 ], [1, 2, 0, -1 ], [1, 0, 2, -1 ], [1, 0, 0, 0 ], [0, 0, 2, 1 ], [0, 2, 0, 1 ],$$ $$ [-1, 3, 1, 2 ], [-1, 1, 3, 2 ], [1, 1, 3, -2 ], [1, 3, 1, -2 ], [1, 2, 2, -2 ], [-1, 2, 2, 2 ], [0, 1, 1, 1 ], [1, 1, 1, -1 ] $$ is a Hilbert basis of the convex cone associated to the fundamental domain returned by the Borcherds’ method, with intersection matrix $$\begin{bmatrix} 0 & 2 & 1 & 5 & 2 & 5 & 1 & 2 & 6 & 6 & 2 & 4 & 4 & 3 & 3 \\ 2 & 0 & 5 & 1 & 2 & 1 & 5 & 6 & 2 & 2 & 6 & 4 & 4 & 3 & 3 \\ 1 & 5 & 2 & 10 & 4 & 14 & 6 & 12 & 20 & 12 & 4 & 8 & 16 & 10 & 6 \\ 5 & 1 & 10 & 2 & 4 & 6 & 14 & 20 & 12 & 4 & 12 & 8 & 16 & 10 & 6 \\ 2 & 2 & 4 & 4 & 0 & 4 & 4 & 8 & 8 & 8 & 8 & 8 & 8 & 4 & 4 \\ 5 & 1 & 14 & 6 & 4 & 2 & 10 & 12 & 4 & 12 & 20 & 16 & 8 & 6 & 10 \\ 1 & 5 & 6 & 14 & 4 & 10 & 2 & 4 & 12 & 20 & 12 & 16 & 8 & 6 & 10 \\ 2 & 6 & 12 & 20 & 8 & 12 & 4 & 4 & 12 & 28 & 20 & 24 & 8 & 8 & 16 \\ 6 & 2 & 20 & 12 & 8 & 4 & 12 & 12 & 4 & 20 & 28 & 24 & 8 & 8 & 16 \\ 6 & 2 & 12 & 4 & 8 & 12 & 20 & 28 & 20 & 4 & 12 & 8 & 24 & 16 & 8 \\ 2 & 6 & 4 & 12 & 8 & 20 & 12 & 20 & 28 & 12 & 4 & 8 & 24 & 16 & 8 \\ 4 & 4 & 8 & 8 & 8 & 16 & 16 & 24 & 24 & 8 & 8 & 8 & 24 & 16 & 8 \\ 4 & 4 & 16 & 16 & 8 & 8 & 8 & 8 & 8 & 24 & 24 & 24 & 8 & 8 & 16 \\ 3 & 3 & 10 & 10 & 4 & 6 & 6 & 8 & 8 & 16 & 16 & 16 & 8 & 6 & 10 \\ 3 & 3 & 6 & 6 & 4 & 10 & 10 & 16 & 16 & 8 & 8 & 8 & 16 & 10 & 6 \end{bmatrix}.$$ Note that all coefficients of this matrix are superior or equal to zero, as expected for an Hilbert basis of a portion of the Nef cone. We thus obtained an Hilbert basis of a chunk of the Nef cone. Possessing such data can be useful in a lot of situations !
We now return to Baragar’s study of the automorphism group of this Wehler $K3$ surface.
We will try to find an answer regarding each transformation $\sigma_i^{\ast}$ described by Baragar.
Baragar indicated that $\sigma_1^\ast$ is either $T_1$ or $S_1 T_1$.
Taking a look at the generating set $\langle g_1,g_2,g_3,g_4,g_5\rangle$ returned by the Borcherds’ method, we see that $$ S_1 T_1 = g_3.$$ Thus, $$\sigma_1^{\ast} = g_3.$$
What about $T_1$ ? It is clear that if $\sigma_1$ is an automorphism, then the image $\sigma_1^{\ast}$ of its action on $\NS(X)$ cannot be represented by two distinct matrices!
Since we just saw that $$\sigma_1^{\ast} = S_1 T_1,$$ we must have $$T_1 \notin \aut(X).$$
Let’s use our function AutTester to check whether $T_1$ fulfills all the requirements for it to be an element of $\aut(X)$.
In case the outcome of this test is False, Prof. Baragar’s interrogations regarding $T_1$ will be settled.
T1 = Matrix([[-1,2,2,0],[0,1,0,0],[0,0,1,0],[-1,1,1,1]])
AutTester(T1)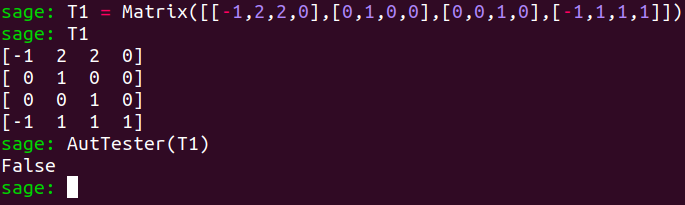
Thus, the matrix $T_1$ clearly cannot be an element of $\aut(X)$.
The Borcherds’ method enables us to assert that Baragar was right regarding $\sigma_1^{\ast}$, since he did indicate that there were two possibilities and that the question had to be settled in this framework. We thus have
$$\sigma_1^{\ast} = S_1 T_1 \in \aut(X)$$.
About $\sigma_2^\ast$, we immediately see that $$\sigma_2^\ast = g_1$$ where $g_1$ is the first generator in the generating set returned by the Borcherds’ method.
Again, Baragar was on point.
Similarly, Prof. Baragar’s automorphism $\sigma_3^\ast$ can be immediately identified as the generator $g_2$ returned by the Borcherds’ method.
Regarding $\sigma_4^\ast$, he indicated that either $\sigma_4^\ast = T_4$ or $\sigma_4^\ast = S_1 \sigma_3^\ast T_4$.
We have $$S_1 \sigma_3^{\ast} T_4 = \begin{bmatrix} -1 & 8 & 0 & 4 \\
0 & 1 & 0 & 0 \\
0 & 10 & -1 & 4 \\
0 & 0 & 0 & 1\end{bmatrix}$$
Let’s determine which one of these transformations satisfies the conditions required for it to be an element of $\aut(X)$ :
AutTester(T4)
We can thus assert with total certainty that $T_4$ is not an element of $\aut(X)$.
Testing the element $S_1 \sigma_3^\ast T_4$ with AutTester must return true. Let’s check if this is indeed the case :
AutTester(S1*sigma3ast*T4)
Let’s prove it by expressing $S_1 \sigma_3^\ast T_4$ as a product of the generators $g_i$ returned by the Borcherds’ method.
At first glance, we cannot decide on this transformation. Let’s dig deeper.
Let’s try a brute force approach. Define
GID = GAMMA + [q.inverse() for q in GAMMA] + [matrix.identity(4)] and remove the eventual duplicates by using the function duplikiller :
GID = duplikiller(GID)Compute the set of words of length 6 in the free group generated by the elements of GID :
WORDS=[(a,b,c,d,e,f,a*b*c*d*e*f) for a in GID for b in GID for c in GID for d in GID for e in GID for f in GID] We now check whether $S_1 \sigma_3^\ast T_4$ can be found in this set of words :
S1*sigma3ast*T4 in [q[6] for q in WORDS]
Great! Let’s retrieve the expression of this transformation as a product of the generators :
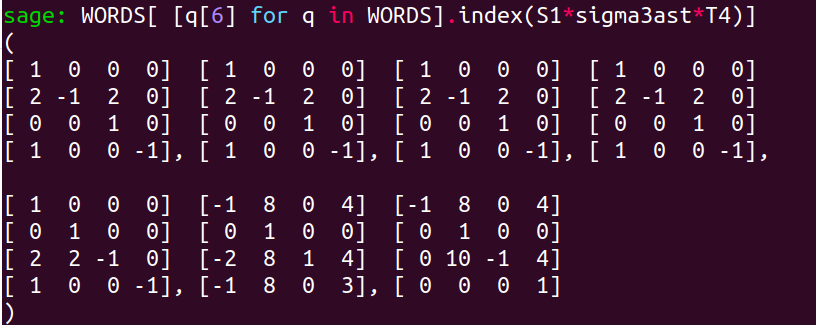
That is, $$S_1 \sigma_3^\ast T_4 = g_1^4 g_2 g_5$$ and since $g_1^4 = \text{Id}$, we obtain $$ \sigma_4^\ast = S_1 \sigma_3^\ast T_4 = g_2 g_5.$$
Thus, the group generated by $$ \langle \sigma_1^\ast,\sigma_2^\ast,\sigma_3^\ast,\sigma_4^\ast\rangle$$ (studied by Baragar) can be expressed as $$ \langle g_3 ,g_1, g_2, g_2 g_5\rangle$$ in terms of the generators of $\aut(X)$ provided by the Borcherds’ method.
The latter enables us to assert that a full generating set of the automorphism group of this Wehler $K3$ with Picard number $4$ is given by $$\aut(X) \simeq \langle g_1, g_2, g_3, g_4, g_5 \rangle$$ with $$g_1= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 2 & -1 & 2 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & -1 \end{bmatrix}, \qquad g_2 = \begin{bmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 2 & 2 & -1 & 0 \\ 1 & 0 & 0 & -1 \end{bmatrix}, \qquad g_3 = \begin{bmatrix} -1 & 2 & 2 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & -1 \end{bmatrix} ,$$ $$g_4 = \begin{bmatrix} -1 & 0 & 8 & 4 \\ -2 & 1 & 8 & 4 \\ 0 & 0 & 1 & 0 \\ -1 & 0 & 8 & 3 \end{bmatrix} ,\qquad g_5 = \begin{bmatrix} -1 & 8 & 0 & 4 \\ 0 & 1 & 0 & 0 \\ -2 & 8 & 1 & 4 \\ -1 & 8 & 0 & 3 \end{bmatrix}.$$
