| $\textbf{Input}$ | $\textbf{Procedure}$ | $\textbf{Purpose}$ | $\textbf{Output}$ |
|---|---|---|---|
| $\text{Chamber}\,\; \mathcal{D}$ $\text{and class}$ $a_0 \in \mathcal{P}_S$ | $\textbf{DegenTest}$ | $\text{Testing whether the}\,\; $ $\mathcal{P}_\mathbb{L}\text{-chamber}$ $\mathcal{D}$ $\; \text{is}$ $\iota(S)\text{-nondegenerate}$ $\text{by determining}$ $\text{whether}$ $\iota(a_0) \in \text{Int}(\mathcal{D}\cap\mathcal{P}_S)$ $\,\;\text{holds}$. | $\text{True / False}$ |
| $m\in \Omega(D) \subset S^{\vee}$ | $\textbf{RatDetect}$ | $\text{Determines whether}$ $(m)^\perp \,\;\text{is a}$ $(-2)\text{-wall of the}$ $\mathcal{P}_S\text{-chamber} \,\;D$ | $ \text{True}\,\; +\,\; \text{class} $ $\text{ / False}$ |
| $m\in \Omega(D) \;\, \text{where}$ $D\,\;\text{has}$ $\text{Weyl vector} \,\; w$ | $\textbf{WeylAdj}$ | $\text{Computes the Weyl }$ $\text{vector}\,\; w^\prime \,\; \text{of}$ $\text{the} \;\,\mathcal{P}_S\text{-chamber}\;\, D^\prime$ $\text{adjacent to the}$ $\mathcal{P}_{S}\text{-chamber} \,\;D$ $\text{along the wall}\,\; (m)^\perp$ | $w^\prime$ |
| $\text{Weyl vector} \;\, w \,\;\text{of}$ $\text{the}\,\;\mathcal{P}_{S}\text{-chamber} \,\;D$ | $\textbf{DeltaW}$ | $\text{Computes the set}$ $\Delta_w \,\; \text{associated to}$ $\text{the} \,\;\mathcal{P}_{\mathbb{L}}\text{-chamber} \,\; \mathcal{D}$ $\text{with}$ $\text{ Weyl vector}\,\; w\in \mathbb{L}$ $\text{such that}$ $D=\mathcal{D}\cap\mathcal{P}_S$ | $\Delta_w$ |
| $\text{Minimal defining set}$ $\text{pr}_{S^\vee}(\Delta_w)\,\; \text{of a}$ $\mathcal{P}_{S}\text{-chamber} \,\;D \,\; \text{with}$ $\text{Weyl vector} \,\; w$ | $\textbf{SetOfWalls}$ | $\text{Computes the}$ $\text{set of walls}$ $\Omega(D) \,\; \text{of}\,\; D$ $\text{by processing the}$ $\text{elements of}$ $\text{the minimal}$ $\text{defining set}$ $\text{pr}_{S^\vee}(\Delta_w)$ | $\text{Set of walls}$ $\Omega(D) \; \, \text{of} \,\; D$ |
| $\text{Set of walls} \,\; \Omega(D)$ $\text{of a }$ $\mathcal{P}_S\text{-chamber} \,\; D$ | $\textbf{AutChamber}$ | $\text{Computes a}$ $\text{generating set }$ $\text{of}\,\;\text{Aut}_{\mathbf{H}}(D)$ | $\text{Generating}$ $\text{set of}$ $\text{Aut}_{\mathbf{H}}(D)$ |
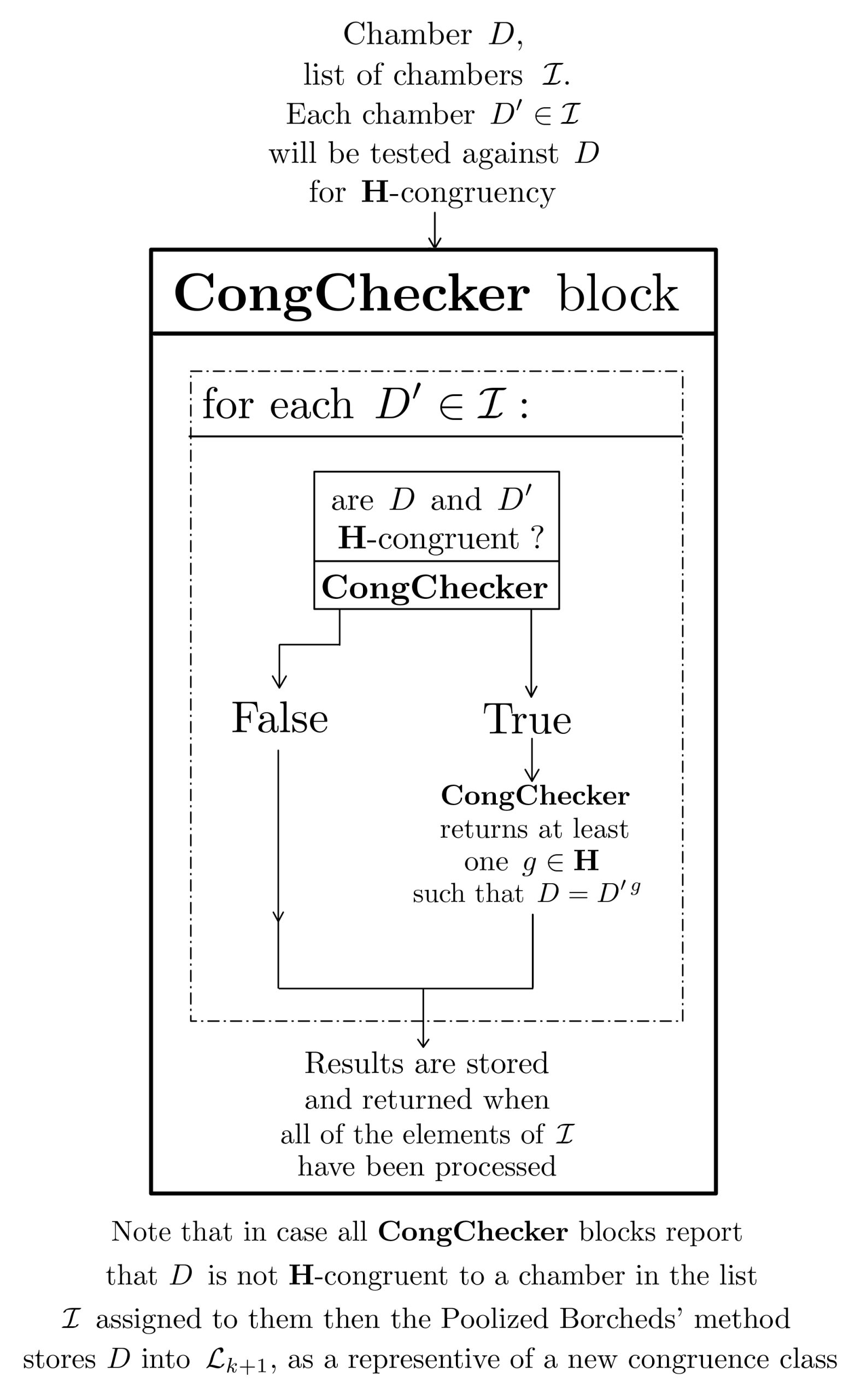
| $\text{Sets of walls}$ $\Omega(D),\,\Omega(D^\prime) \,\; \text{of}$ $\mathcal{P}_S\text{-chambers} \,\; D,\,D^\prime$ | $\textbf{CongChecker}$ | $\text{Determines whether}$ $ D \,\; \text{and} \,\; D^\prime$ $\text{are}\,\; \mathbf{H}\text{-congruent.}$ $\text{When this is}$ $\text{the case, returns}$ $\text{at least one}$ $g\in \mathbf{H} \,\; \text{such}$ $\text{that}\,\; D^\prime = D^g$ | $\text{True}\,\;+ $ $ \text{element of} \,\;\mathbf{H}$ $ / \,\; \text{False}$ |
| $(\rho \times \rho)\text{-sized}$ $\text{matrix}\,\; M$ $\text{where} $ $ \rho = \text{rank}(\text{NS}(X))$ | $\textbf{MemberCrit}$ | $\text{Tests whether}$ $\text{the matrix}\,\; M$ $\text{represents}$ $\text{a transformation}$ $g\in \mathbf{H}$ | $\text{True / False}$ |
| $\text{Embedding}$ $\iota : S \hookrightarrow \mathbb{L},$ $\text{element} \,\; a_0 \in \mathcal{P}_S$ $\text{and}$ $\mathcal{P}_{\mathbb{L}}\text{-chamber }\mathcal{D}$ $ \text{which fails}$ $\textbf{DegenTest}\,\; \text{i.e.} \,\;\mathcal{D}$ $\text{cannot be} $ $\text{asserted as}$ $\iota (S)\text{-nondegenerate}$ | $\textbf{EmbUpdater}$ | $\text{Updates}$ $\text{the embedding}$ $\iota : S\hookrightarrow \mathbb{L} \,\; \text{to produce}$ $\text{an embedding}$ $\iota_\text{upd} : S\hookrightarrow \mathbb{L}$ $\text{under which}$ $\iota_{\text{upd}}(a_0) \in \text{Int}(\mathcal{D}\cap\mathcal{P}_S) $ $\text{holds. That is,} $ $\text{the chamber}\,\; \mathcal{D}\,\; \text{is} $ $\iota_{\text{upd}}(S)\text{-nondegenerate}$ | $\text{Updated}$ $\text{embedding}$ $\iota_\text{upd} : S\hookrightarrow \mathbb{L}$ |
| $\text{Initial embedding}$ $\iota : S\hookrightarrow \mathbb{L}$ | $\textbf{KerChecker}$ | $\text{Determines whether}$ $-1\notin \text{Ker}(\eta_T) \,\; \text{holds}$ | $\text{True / False}$ |
Here is a diagram illustrating the algorithmic structure of the classical Borcherds’ method, which involves most of the above-mentioned procedures : Assume that the Borcherds’ method accomplished its $k$-th iteration. Denote by $\mathcal{L}_k$ the set of chambers of level $k$ each representing their own congruence class of chambers and identified during the $k$-th iteration.

The Poolized Borcherds’ method is a modernized version of the Borcherds’ method which fully takes advantage of process-based parallelism :