July 2 – The programs have been updated.
This page will soon be updated accordingly
The program PModChecker will enable you to determine if a class in the Néron-Severi group of your $K3$ surface $X$ can be associated with a projective model of $X$ in virtue of Morrison’s theorem.
We could demonstrate PModChecker by using CGS to generate datasets of classes of square $2,4,6$ or $8$, and we could then pick classes in this dataset and test them with PModChecker.
That would be OK, but the result wouldn’t be worth much.
What would be the point of generating tons of results devoid of geometric interpretation?
Let’s follow an approach developed by Xavier Roulleau in his atlas of K3 surfaces and this paper On the geometry of K3 surfaces with finite automorphism group and no elliptic fibrations.
To study projective models of a $K3$ surface while emphasizing the geometric aspect, XR enforces a technique that consists in using the data produced by his program to handcraft a configuration of smooth rational curves associated with an ample class, for example
$$\begin{cases} C_{1}+C_{2}=D\\C_{3}+C_{4}=2D \end{cases}$$
where $C_1,C_2,C_3$ and $C_4$ are classes of smooth rational curves and where $D$ an ample, base-point free and non-hyperelliptic class such that $D^2 =4$. We call such a configuration a system.
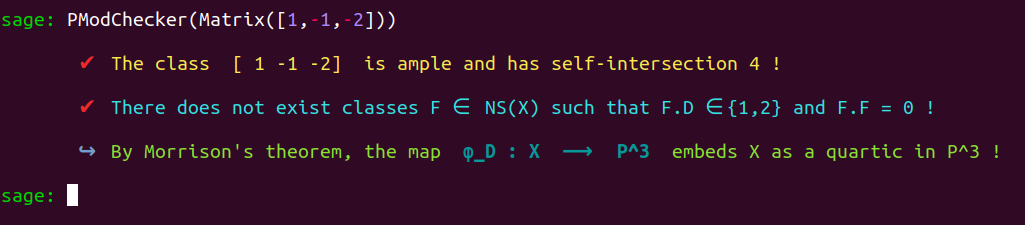
Morrison’s theorem tells us that the morphism $$\varphi_D : X\longrightarrow \mathbb{P}^3$$ embeds $X$ as a quartic surface.
In this context, the above mentioned configuration has a very precise geometric interpretation : $$C_1 + C_2 = D$$
can be interpreted as an hyperplane section of a quartic in $\mathbb{P}^3$ which decomposes as the union of smooth rational curves of respective degrees $C_1 \cdot D$ and $C_2 \cdot D$, while $$C_3 + C_4 = 2D$$
can be seen as a conic section of a quartic which decomposes as the union of smooth rational curves $C_3$ and $C_4$ of respective degrees $C_3 \cdot D$ and $C_4 \cdot D$.
Simple computations involving dimensions of linear systems make it possible to determine whether a quartic in $\mathbb{P}^3$ containing such a configuration exists.
By Saint-Donat and Morrison, the base point freeness and non-hyperellipticity of an ample class $D$ of self-intersection $4$ are equivalent to the non-existence of classes $F$ such that $F^2=0$ and $F \cdot D \in {1,2}$.
With this approach in mind, we have produced the programs SysFinder and SysDisplay : These programs enable us to first determine a configuration $$\begin{cases} C_{1}+C_{2}=n_1 D\\C_{3}+C_{4}=n_2 D \end{cases}$$
with ll $D$ of square $2,4,6$ or $8$ and the $C_{i}’s$ classes of smooth rational curves on X.
We present these programs on an example and will then use PModChecker to determine whether the class $D$ has an associated morphism realizing $X$ in projective space as specified in the SDM theorem.
Please download the following input data file: INPUT_DATA_PICARD_THREE_XT_t_=_7.sobj
We will study projective models of the $K3$ surface $X$ with Néron-Severi group $S=\text{NS}(X)$ isomorphic to the lattice with Gram matrix $$G_S = \begin{bmatrix} 14 & 0 & 0 \\ 0 & -2 & 0 \\ 0& 0 & -2 \end{bmatrix}.$$
Open a Sage console from the folder into which you stored the file. Enter these commands
INPUT_DATA=load('INITIAL_INPUT_DATA_xt_picard_three_case_7.sobj');
GramMatS = INPUT_DATA[0];
amp0 = INPUT_DATA[2];
and load PModChecker.sage :

The program asks us to compute
ListSRC = CGS(MaxDegree=30000,GramMatrix=GramMatS,Ample=amp0,SelfInt=-2)
That is, we use CGS in order to compute the set of classes of smooth rational curves $r\in \text{NS}(X)$ such that $r\cdot a_0 \leq 30000$, where we denote amp0 by $a_0$.
We then define
ListSRCred=ListSRC[:25]which is the list of the first 25 elements of ListSRC, where you can replace $25$ by a more suitable value in case the cardinality of ListSRC is smaller than $25$.
We then reload PModChecker.sage, and this time you should not see any warning displayed.

The function SysFinder takes the three following mandatory parameters as input data :
- GramMatrix : Gram matrix of $S=\text{NS}(X)$,
- ample : ample class,
- selfint : integer,

and returns the raw data of all linear combinations of the form $$C + C^{\prime} = nD$$ with $C,C^{\prime}$ distinct classes of smooth rational curves in ListSRCred, with $D$ a class of self-intersection selfint such that the intersection product $D\cdot a_0 $ inferior or equal to mdpar.
SysFinder will save the data it computes in a dedicated file

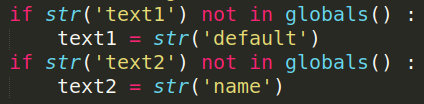
You can personalize the name of this file by defining global string variables text1 and text2. For example,
text1 = str('my_surface')
text2 = str('picard_3')Otherwise, text1 and text2 will be set by default as
Let’s compute all the possible linear combinations $$C + C^{\prime} = nD$$ with $D^2 = 4$ and $D\cdot a_0 \leq 5000$, where $5000$ is the default value of mdpar, and such that $C$ and $C^{\prime}$ in ListSRCred.
Define
SYSTEMS = SysFinder(GramMatrix=GramMatS,ample=amp0,selfint=4)Then, run
SysDisplay(SYSTEMS)The program SysDisplay will then use the data from SYSTEMS to form configurations
$$\begin{cases} C_{1}+C_{2}=n_1 D\\C_{3}+C_{4}=n_2 D \end{cases}$$
associated to an ample class $D$ of square $4$, and will display one of them, chosen randomly among the various possibilities, for example :
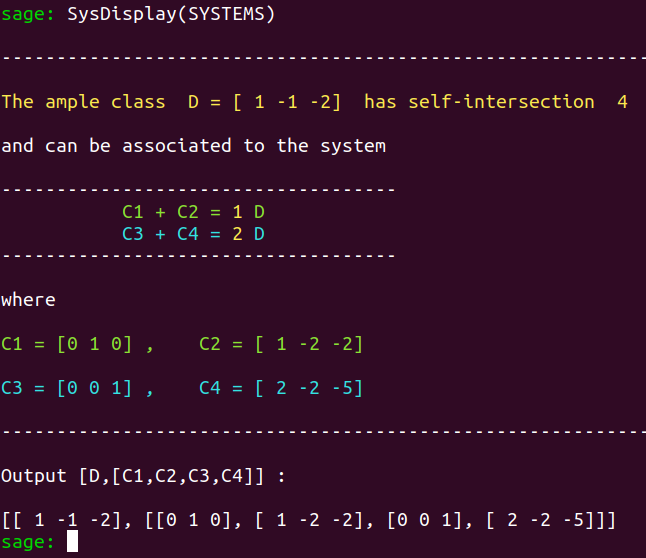
That is, the program returned a configuration
$$\begin{cases} C_{1}+C_{2}=D\\C_{3}+C_{4}=2D \end{cases}$$
associated to the ample class $[1,-1,-2]_S$ of self-intersection $4$.
with $$C_1 = [0,1,0]_S, \qquad C_2=[1,-2,-2]_S ,$$ $$C_3 = [0,0,1]_S , \qquad C_4 = [2,-2,-5]_S .$$
Let’s use PModChecker to determine if a projective model of the surface under study can be exhibited from the data of $D$ in virtue of Morrison’s theorem :
PModChecker(Matrix([1,-1,-2]))