Here are a few nice pictures of graphical representations of the fundamental domain of the action of $\text{Aut}(X)$ onto $\text{Nef}(X)\cap \mathcal{P_S}$ for some $K3$ surfaces $X$ with Picard number $3$, where we denote by $S=\text{NS}(X)$ the Néron-Séveri group of $X$ and by $\mathcal{P}_S$ its positive cone.
Note that these representations are generated thanks to a program which takes advantage of Pyplot’s elementary features. Also, note that a tangible and meaningful interpretation can thus be associated to the notion of chamber structure for cases in Picard number $3$.
Red lines depict boundary walls, while purple lines depict boundary $(-2)$-walls.
Fundamental domain of the action of $\text{Aut}(X)$ onto $\text{Nef}(X)\cap \mathcal{P_S}$ when the Néron-Severi group $S$ of the $K3$ surface $X$ under study has Gram matrix $$ \begin{bmatrix} 30 & 0 & 0 \\ 0 & -2 & 1 \\ 0 & 1 & -2 \end{bmatrix}$$
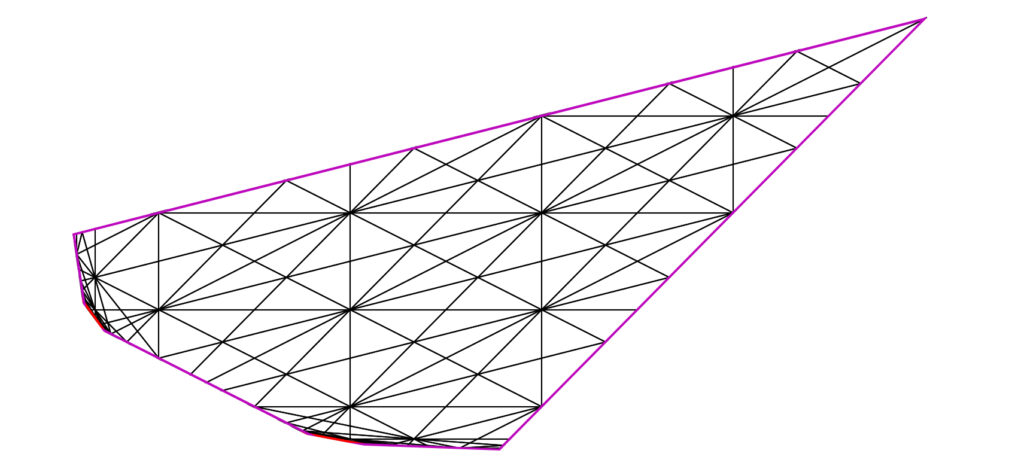
Fundamental domain of the action of $\text{Aut}(X)$ onto $\text{Nef}(X)\cap \mathcal{P_S}$ when the Néron-Severi group $S$ of the $K3$ surface $X$ under study has Gram matrix $$ \begin{bmatrix} 20 & 0 & 0 \\ 0 & -2 & 1 \\ 0 & 1 & -2 \end{bmatrix}$$

Fundamental domain of the action of $\text{Aut}(X)$ onto $\text{Nef}(X)\cap \mathcal{P_S}$ when the Néron-Severi group $S$ of the $K3$ surface $X$ under study has Gram matrix $$ \begin{bmatrix} 14 & 0 & 0 \\ 0 & -2 & 1 \\ 0 & 1 & -2 \end{bmatrix}$$

Fundamental domain of the action of $\text{Aut}(X)$ onto $\text{Nef}(X)\cap \mathcal{P_S}$ when the Néron-Severi group $S$ of the $K3$ surface $X$ under study has Gram matrix $$ \begin{bmatrix} 14 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & -2 \end{bmatrix}$$
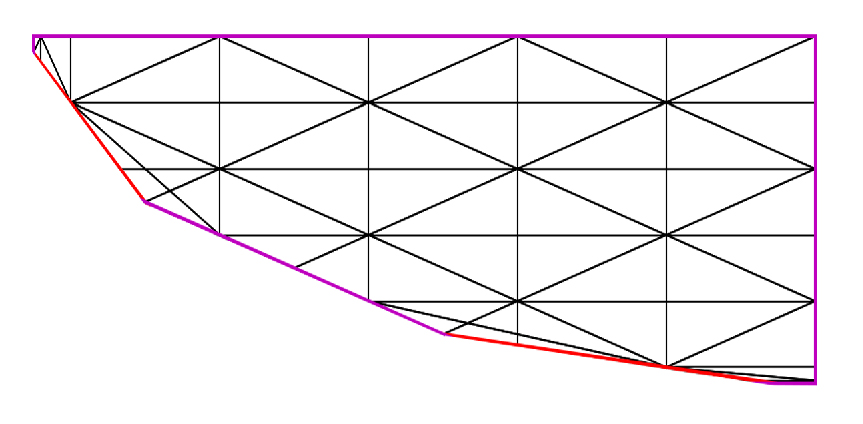
Fundamental domain of the action of $\text{Aut}(X)$ onto $\text{Nef}(X)\cap \mathcal{P_S}$ when the Néron-Severi group $S$ of the $K3$ surface $X$ under study has Gram matrix $$ \begin{bmatrix} 4 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & -2 \end{bmatrix}$$

Fundamental domain of the action of $\text{Aut}(X)$ onto $\text{Nef}(X)\cap \mathcal{P_S}$ when the Néron-Severi group $S$ of the $K3$ surface $X$ under study has Gram matrix $$ \begin{bmatrix} 4 & 0 & 0 & 0\\ 0 & -2 & 0 &0\\ 0 & 0 & -2 &0 \\ 0 & 0 & 0 & -2\end{bmatrix}$$


As displayed on the other figures, walls in cases in picard 3 can be represented by lines in the plane. When dealing with cases in Picard 4, walls are hyperplanes in three-dimensional space. For cases in Picard $N$, walls are realized as hyperplanes in $N-1$ dimensional space.
