Cloud

A private cloud computing server with an allocation of 8 logical cores / 24GB ram,
fully loaded with all the material produced during this thesis
and running 24/7 is at the disposal of the reviewers of this thesis.

If you need access to the server or the programs, feel free to contact us.

Remark: An archive ThesisPrograms.zip containing
all the programs has also sent to reviewers on April 30.
Moreover, login information to access the server and unlock
restricted sections of this website has been sent to reviewers on April 30.

Remark, June 2: An updated ThesisPrograms folder, named ThesisProgramsJune, that contains the programs needed to run examples on BM & Parallelism, Congruence Testing, etc… has been uploaded to the demo server.

NB: Once connected to the server, you can download the ThesisProgram folder with an scp command, e.g.:

scp -r username@hostname:/home/username/ThesisPrograms LocalArrivalFolderOnYourComputer

Once you are connected to the server, please proceed as follows :

Move into the folder ThesisPrograms

cd ThesisPrograms

We already installed a Conda environment with Sage 9.2 using Python 3.8.5.

Magma is also installed and operational.

This environment replicates the exact environment in which we worked during our thesis.

Activate this environment by using the command :

conda activate sage

You can then run Sage simply by entering :

sage

We provide ready-to-use input data for a lot of surfaces. You will thus be able to compute a generating set of $\text{Aut}(X)$ (among many other things !!!) for a considerable number of surfaces!

We will also soon provide an archive with all the results we obtained during our studies regarding the “automorphism” part of our thesis, i.e., all the data produced by the programs related to Borcherds’ method.

The study of the following family of surfaces in Picard number $3$ was the initial goal of this thesis :

  • Family of surfaces with Néron-Severi group having Gram matrix $$ \begin{bmatrix} 2t & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & -2 \end{bmatrix}$$ with respect to a fixed basis for $1< t \leq 50$.
  • We also provide input data for the Picard $4$ et $5$ analogs of these surfaces, with input data respectively stored in 
INPUT_DATA/DIAG_PICARD_FOUR/

and

INPUT_DATA/DIAG_PICARD_FIVE/

You will also find input data on classics such as :

$$ \begin{bmatrix} 0 & 2 & 2 \\ 2 & 0 & 2 \\ 2 & 2 & 0 \end{bmatrix}$$ 

INPUT_DATA = load('INPUT_DATA/WEHLER_K3_SURFACES/INPUT_DATA_WEHLER_PICARD_THREE.sobj')

$$ \begin{bmatrix} 0 & 2 & 2 & 0 \\ 2 & 0 & 2 & 1 \\ 2 & 2 & 0 &1 \\ 0 & 1 & 1 & -2 \end{bmatrix}$$

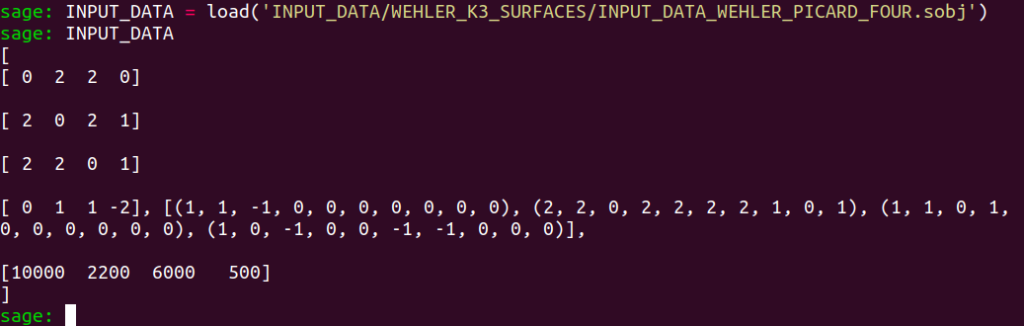
NB: You will see that our programs confirm all the results announced by Prof. Baragar and even more!

You can set nb_workers = 8
before launching a computation.

Note that the default value assigned to nb_workers equals one-half the number of logical cores on your CPU. Regarding our demo server, which has been allocated eight cores, the default value for nb_workers is set to 4. You can assign a larger value, e.g. 24, to this variable and achieve a positive effect.

Once an input data list is specified, you can directly run the Poolized Borcheds’ method by entering :

load('borcherds_direct.sage')

Before doing so, note that you can personalize the names of the folder and various files created by Borcherds’ method: text events reports, data of chambers, generators, representatives of orbits of (-2)-curves, and recovery data.

NB: In case of a crash, power outage…
This data will enable you to start the computation from the exact point at which it was interrupted. Note that we haven’t explained yet on this website how to use the recovery feature of our implementation of the Borcherds’ method.

To do so, assign a value of your choice to strings text1 and text2, for example, 

text1 = str('Baragar_Wehler')
text2 = str('picard_3')

so that all data produced will have a name looking like

some_data_Baragar_Wehler_picard_3

following the convention explained on this page. Otherwise, random words will be assigned to text1 and text2, giving files and folders with terms such as

NB1: All programs will be released in public access the day after the defense.

NB2: 8 logical cores / 24GB ram is enough to run a lot of examples and perform experiments comfortably. A dedicated workstation with a 5950X and 128GB of ram was used to perform most of the computations during the last months of this thesis.

NB3: Obviously, k3su.com and the demo server run on separate machines. The demo server is 100% dedicated to the reviewers and fully backed up regularly,
so that there is no issue at all in case you break it, it will be restored.