NB: Screenshots have to be updated; instead of talking about “logical cores”, it is better to use the term “workers.”
On this page, we explain how to execute the Poolized Borcherds’ method on an example. The Poolized Borcherds’ method uses process-based parallelism to deploy its internal procedures in parallel. To this end, a pool of workers is created with the Pool object from the Python multiprocessing library.
- Review of the preliminary steps.
- Naming convention regarding the various files produced by the method.
- Launching Borcherds’ method.
As before, we study the $K3$ surface $X$ with Néron-Severi group $S=\text{NS}(X)$ having Gram matrix
$$G_S=\begin{pmatrix}4 & 0 & 0\\ 0 & -2 & 0\\0 & 0 & -2\end{pmatrix}$$ with respect to a fixed basis. Load the associated input data into a Sage session :
INPUT_DATA = load('INPUT_DATA/DIAG_PICARD_THREE/INPUT_DATA_DIAG_PICARD_THREE_case_2.sobj')Recall that we have previously seen how to :
- Set up the basic environment to pursue our studies.
- Determine whether the Borcherds’ method will return a generating set of $\text{Aut}(X)$.
- Update an initial embedding to provide a suitable initial chamber to the method.
Before proceeding to the execution of the Borcherds’ method, we start by reviewing these preliminary steps.
Preliminary steps
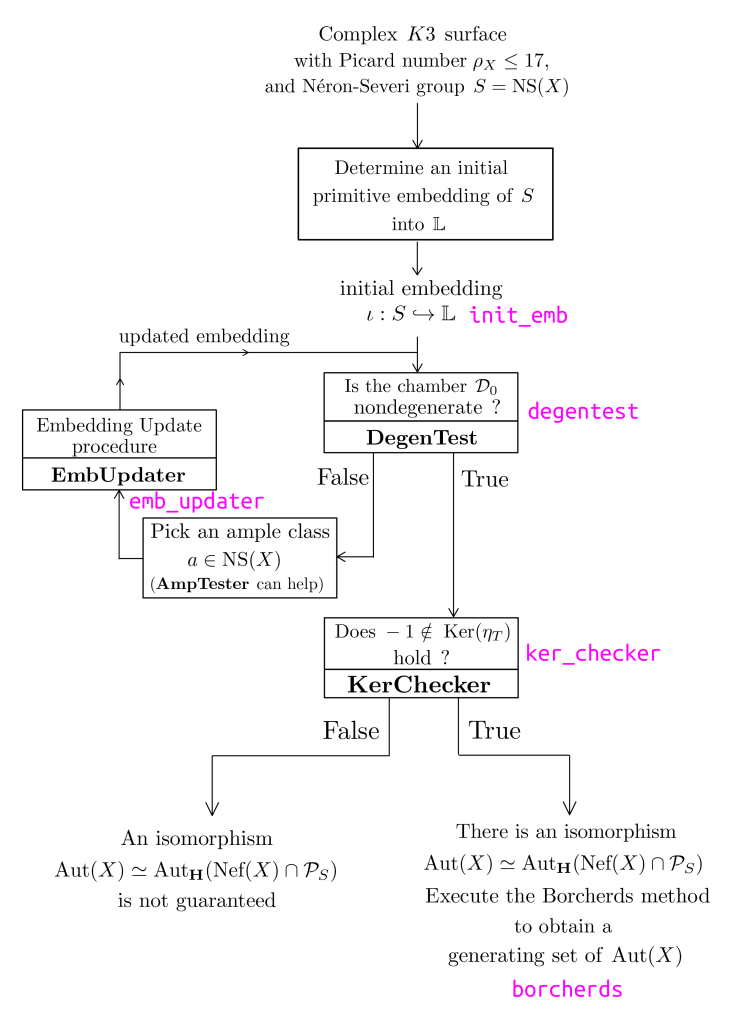
Load init_emb to embed $S$ into $$\mathbb{L} = U\oplus E_{8}(-1)$$ and initialize an environment adapted to the study of $X$ : declaration of variables, essential functions, modules from libraries…
load('init_emb.sage')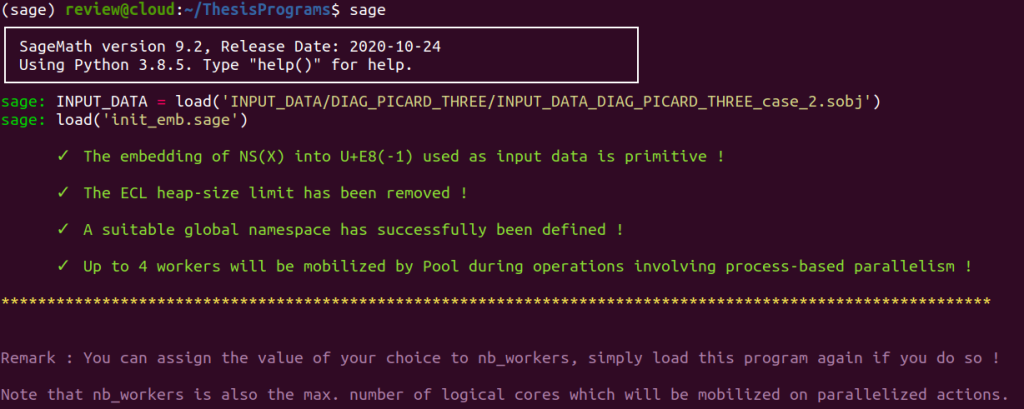
Note that you can specify the maximum number of workers used by Pool on parallelized operations. For example, the demo server has an allocation of 8 cores, i.e., os.cpu_count() equals 8.
os.cpu_count()You can thus set nb_workers = 8.
The machine will thus ideally be able to process each one of the worker processes on a dedicated logical core. Load ker_checker to determine whether the method will return a generating set of $\text{Aut}(X)$ :
load('ker_checker.sage')
Load degentest to determine whether the initial primitive embedding obtained from the vectors specified in INPUT_DATA[1] defines an initial chamber under which a suitable initial chamber can be provided to the Borcherds’ method for it to be executed :
load('degentest.sage')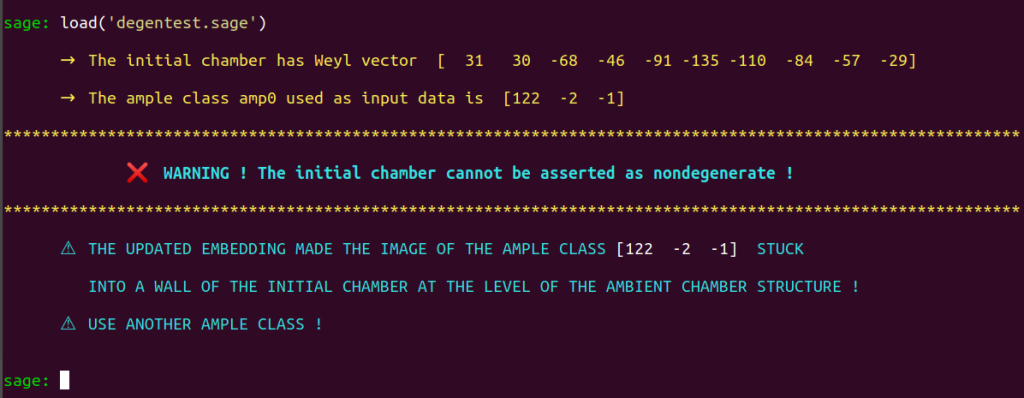
We have already seen that the embedding defined by this vector and the ample class in INPUT_DATA do not succeed degentest. We thus have to update the embedding.
To this end, load emb_updater:
load('emb_updater.sage')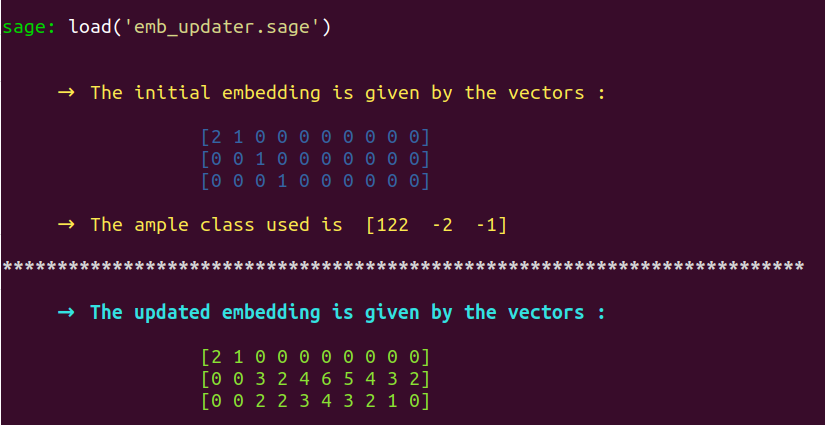
An updated embedding is then returned. We use degentest again to check whether this updated embedding makes the initial chamber have the desired property of containing in its interior the image of the ample class specified in INPUT_DATA[2] and declared under the name amp0 :
load('degetest.sage')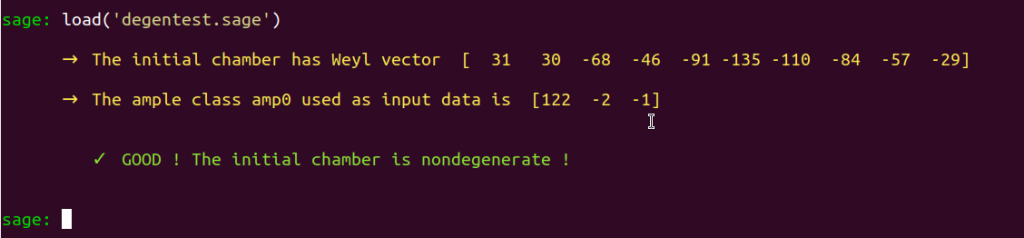
We are now ready to execute Borcherds’ method.
The following figure summarizes all the preliminary steps which had to be taken until now :
Naming the data files produced by the method
Our implementation of the Borcherds’ method will produce many data files: Raw data, generators, representatives of orbits of smooth rational curves, data tuples of chambers, monitoring data, text event reports, and logs… These data files are stored in a dedicated folder created by the method as soon as it is executed. You can personalize the name of this folder according to the following convention :
Declare two string variables text1 and text2, each assigned the name of your choice.
For example, if you define
text1 = str('my_surface')
text2 = str('case_2')then a folder
will be created and used by the Borcherds’ method to store various files produced during its execution, such as :
Detailed explanations regarding the purpose of each one of the data files created by the Borcherds’ method are provided on this page.
If you do not specify your strings for text1 and text2, words chosen from a list of approximately 60.000 English words will be randomly assigned to these variables.
Lauching the Borcherds’ method
We are now ready to execute Borcherds’ method by loading the borcherds.sage program :
load('borcherds.sage')Starting from the initial $\mathcal{P}_S$-chamber, te Borcherds’ method explores and processes the $\mathcal{P}_S$ chamber structure over $\text{Nef}(X)\cap\mathcal{P}_S$, moving level by level by crossing adjacencies along non $(-2)$-walls, until a complete set of representative of $\text{Aut}(X)$-congruence classes of $\mathcal{P}_S$ chambers contained in $\text{Nef}(X)\cap\mathcal{P}_S$ has been obtained.
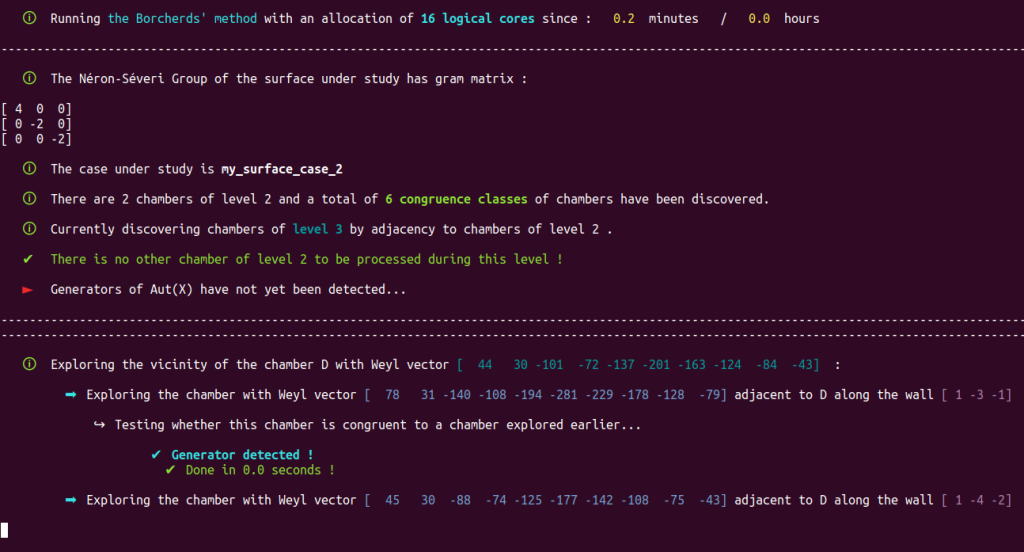
Dealing with the case under study is usually a matter of less than 60 seconds, at worse.
Here is the result of the execution of the Borcherds’ method, launched on our demo server intended for the reviewers of this thesis :
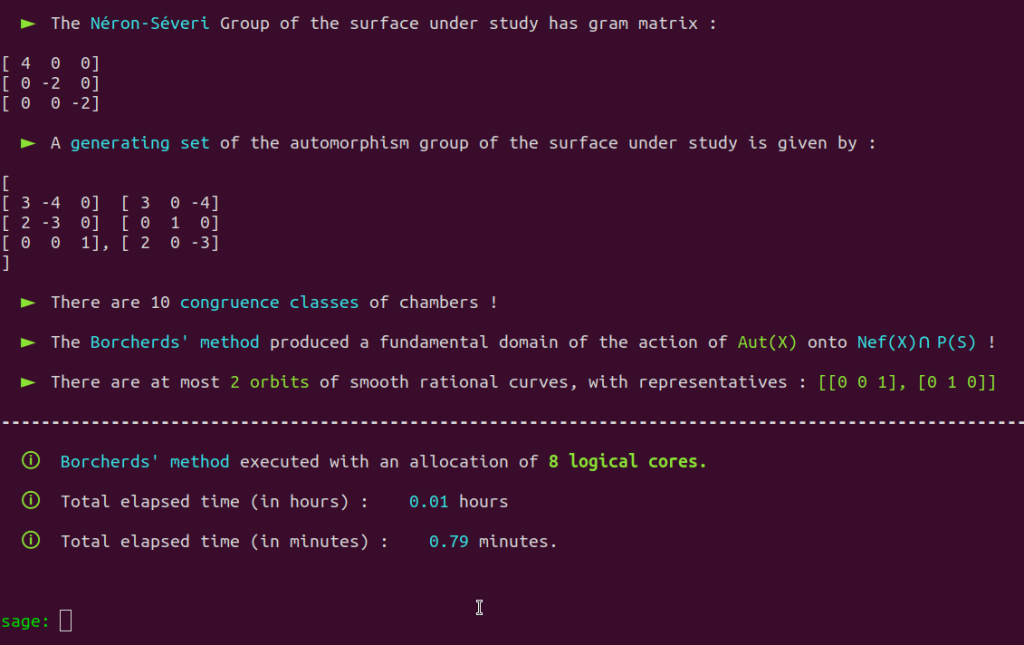
The set
$$\{ \begin{pmatrix}3 & -4 & 0\\2 & -3 & 0\\0 & 0 & 1\end{pmatrix},\begin{pmatrix}3 & 0 & -4\\0 & 1 & 0\\2 & 0 & -3 \end{pmatrix}\}$$
is therefore a generating set of the automorphism group of the $K3$ surface having Néron-Severi group isomorphic to the lattice with Gram matrix
$$G_S=\begin{pmatrix}4 & 0 & 0\\ 0 & -2 & 0\\0 & 0 & -2\end{pmatrix}.$$
About the output data within the console :
- The variable GAMMA is assigned to the list containing the generators of $\text{Aut}(X)$.
- The variable REAL_RAT is assigned to the list of representatives of the orbits of classes of smooth rational curves on $X$ under the action of $\text{Aut}(X)$.
- The variable LOSOC is assigned to the list of lists of chambers, sorted by level.
That is, LOSOC[0] contains the data of the representatives of level $0$ and thus only includes the data tuple associated with $D_0$. The list LOSOC[1] contains the data tuples of representatives of level $1$, the list LOSOC[2] is the list of data tuples of representatives of level $2$, etc…
One last thing: Provided that all the requirements of each step are satisfied, you can start from
INPUT_DATA = load('INPUT_DATA/DIAG_PICARD_THREE/INPUT_DATA_DIAG_PICARD_THREE_case_2.sobj')and run all the programs in one shot by using
load('borcherds_direct.sage')