Parallelism - PT. 2 - K3surfaces.com

All the material presented on this page can be executed on the demo server. However, an allocation of eight logical cores clocked at 2.1 GHz does not provide enough processing power to comfortably run our PFB / APFB two-dimensional parallel strategy. Remember that we want each process, Master or Auxiliary, to be capable of mobilizing its own pool of worker processes, say, eight worker processes.

Remember that using a scalable cloud computing service may be the best solution for you. For example, a well-known European provider of cloud services offers a plan providing access to 48GB ram / 24 logical cores for a cost of 0,60€ per hour of use, including VAT.

We used our dedicated workstation to perform all the computations presented on this page. Computations involving PFB / AFB can be identified thanks to the mention “parallelized exploration enabled” at the top of the screen, that is,

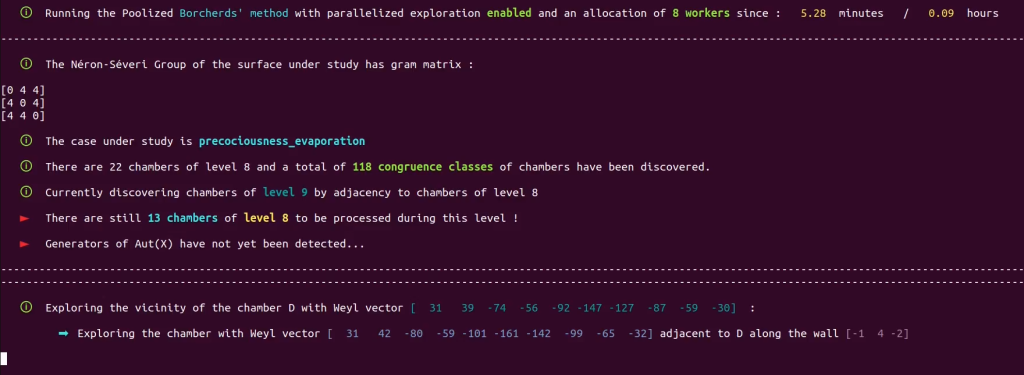
Here is a short video showing the various processes running in parallel during the study of the $K 3$ surface mentioned in the above screenshot. We can see at 00:12 the PFB-enhanced primary process (Poolized Borcherds’ method executed with PFB = True) method supported by four auxiliary APFB processes. (AFPB n°1, 2, 3, and 4) :

Example of computation mobilizing four auxiliary APFB processes. Each process can also mobilize its own pool of eight worker processes. A text file is updated in real-time whenever the Primary process directly obtains the data of a set of walls, thanks to the work of an APFB process.

Very Important: Note that we explain on the Network deployment page how to enforce this strategy at the network level to mobilize the processing power of more than one physical machine to execute the Borcherds’ method.

Define the input data list associated with the $K 3$ surface under study by entering

INPUT_DATA=load('INPUT_DATA/DEMO/INPUT_DATA_DEMO_PFB.sobj')

The Poolized Borcherds’ method is PFB-ready. At the code level, setting

PFB = True

before executing the method results in a swap of the Walls computation Block from the Poolized Borcherds’ method for a Poolized Functional Block (PFB). The latter will enable the method to communicate with processes executing an Autonomous Poolized Functional Block.

We enforce the strategy described in this figure in the case where $N = 3$ , that is :

We execute an instance of the PFB-enhanced Poolized Borcherds’ method, which will play the role of the primary process $P_{0}$ .
Assume that the primary process $P_{0}$ is exploring and processing the adjacencies of level $k$ , i.e., $P_{0}$ discovers chambers of level $k + 1$ . We launch three APFB processes $P_{1}, P_{2}$ and $P_{3}$ in charge of assisting the primary process by exploring the adjacencies of chambers of level $k$ , and computing the sets of walls of chambers of level $k + 1$ thus discovered.
Still assuming that $P_{0}$ is exploring and processing the adjacencies of chambers of level $k$ , we launch an extra APFB process $P_{4}$ in charge of exploring and processing the adjacencies of chambers of level $k + 1$ as soon as these chambers are identified as new congruence classes of chambers of level $k + 1$ by $P_{0}$ . The process $P_{4}$ thus computes sets walls of chambers of level $k + 2$ during the $k$ -th iteration of the method. That is, the process $P_{4}$ gets a head start on the work to be done during the next iteration.

At the beginning of each iteration, say the $k$ -th, the primary process $P_{0}$ splits evenly the workload contained in $L_{k}$ into three chunks so that $P_{1}$ , $P_{2}$ and $P_{3}$ each receive their share of the workload. The process $P_{4}$ closely monitors the state of the set $L_{k + 1}$ which contains representatives of congruence classes of chamber $k + 1$ discovered during the $k$ -th iteration and computes the sets of walls of their adjacencies as soon as they are added into this set (FIFO).

The processes are synchronized by level : $P_{0}$ , $P_{1}$ , $P_{2}$ and $P_{3}$ all work at the same level, while $P_{4}$ works one level higher. The situation can be illustrated as follows :

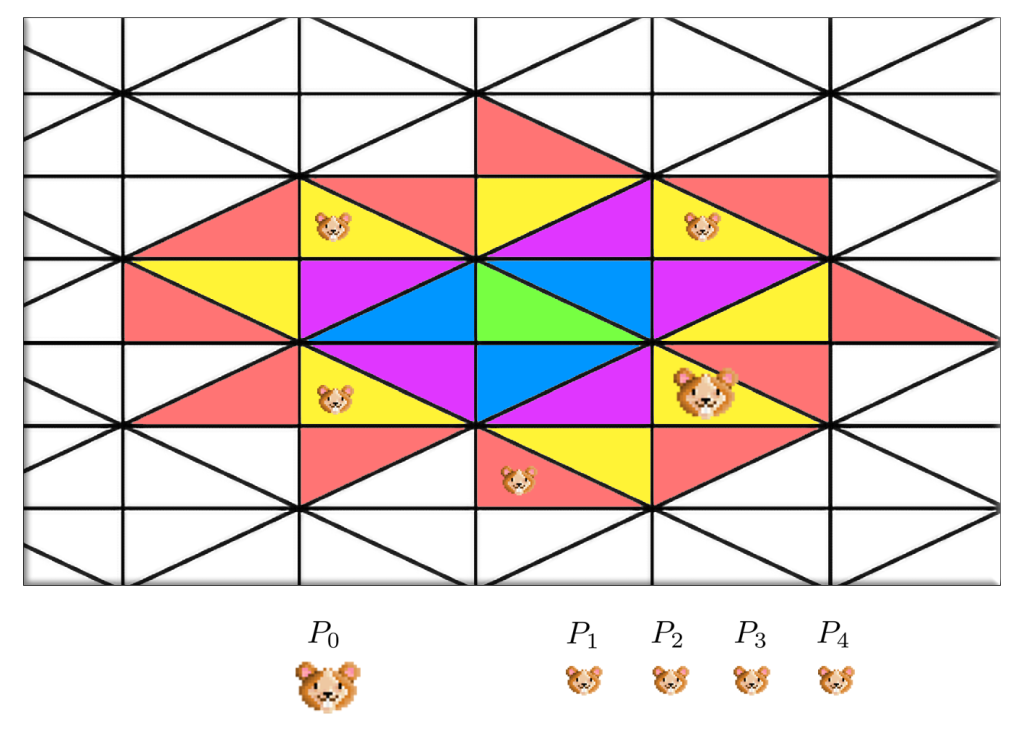
The giant hamster is the primary process; there are three auxiliary APFB processes, each focusing on their assigned share of the workload and located at the same level as the primary process (yellow chambers). There is an additional auxiliary APFB one level higher, getting ahead of the work to be done during the next iteration.

We proceed by explaining, one by one, the following points :

Launching the primary process $P_{0}$ : PFB-enhanced instance of the Poolized Borcherds’ method.
Launching APFB processes $P_{j}$ for $j = 1, 2, 3$ .
Launching the extra APFB process $P_{4}$ .

We thus enforce for $N = 3$ the PFB / APFB strategy illustrated below

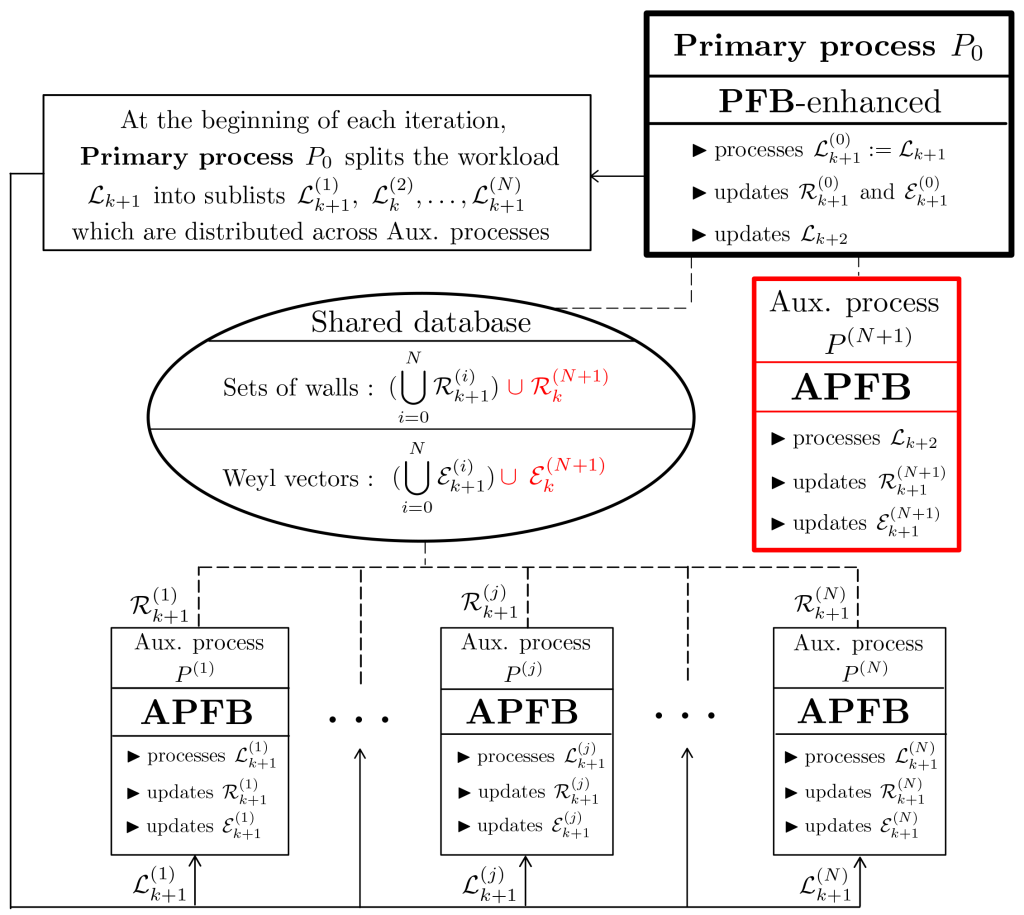
Launching $P_{0}$

We start by launching the primary process $P_{0}$ :

INPUT_DATA=load('INPUT_DATA/DEMO/INPUT_DATA_DEMO_PFB.sobj')
PFB = True
nb_workers = 8
load('borcherds_direct.sage')

Note that $P_{0}$ is thus allowed to mobilize its own pool of eight worker processes to execute its internal procedures in parallel. These workers are not related to the processes $P_{1}, P_{2}, P_{3}$ or $P_{4}$ .

Note that the implementation of Borcherds’ method will, by default, assume that the user will launch $3$ APFB processes to split the workload to be processed during each iteration. For example, at the beginning of the $(k + 1)$ -th iteration, the splitting of the workload is performed by the function ChunkMaster, which splits $L_{k}$ fairly into nb_chunks subsets when (obviously) the set $L_{k}$ a cardinality superior or equal to nb_chunks.

Code from **parallelized_borcherds.sage** -The function **ChunkMaster** splits the workload evenly into nb_chunks subsets so that a chunk can be assigned to each auxiliary process.

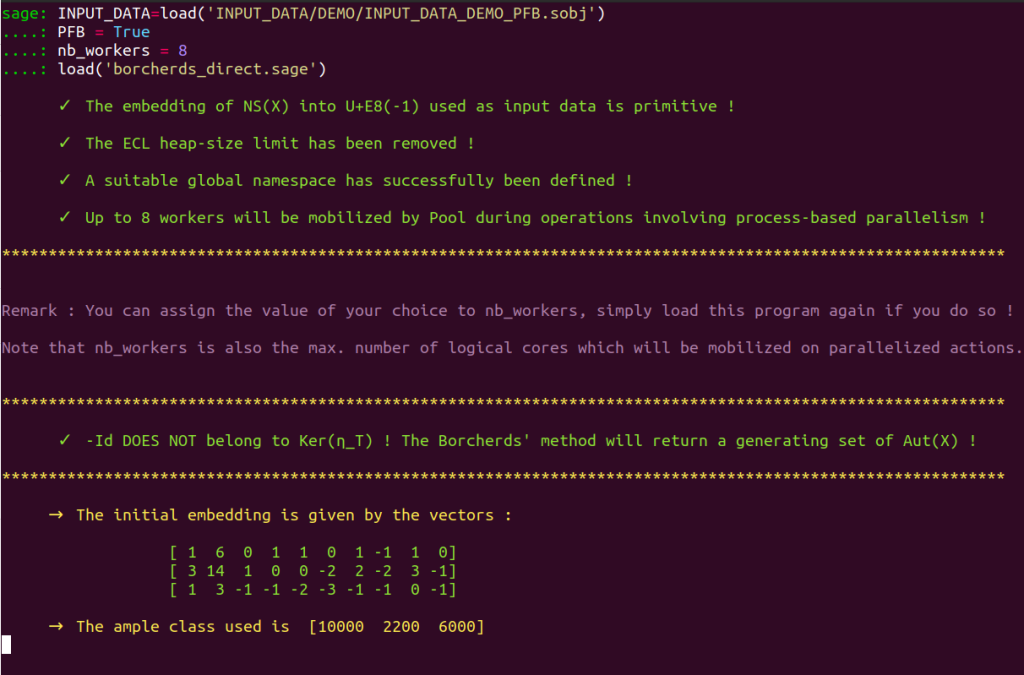
The method starts its execution :

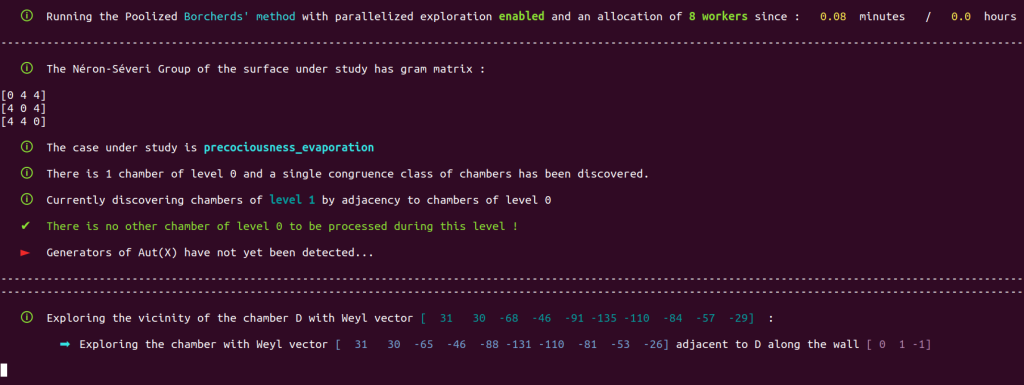
Since we did not assign values to text1 and text2 before executing the method, string values were picked randomly and assigned to these variables. We see on the screenshot just above that

text1 is str(‘precociousness’)

and that

text2 is str(‘evaporation’)

For example, to launch the primary process $P_{0}$ with these values for text1 and text2, use

text1 = str('precociousness')
text2 = str('evaporation')
INPUT_DATA=load('INPUT_DATA/DEMO/INPUT_DATA_DEMO_PFB.sobj')
PFB = True
nb_workers = 8
load('borcherds_direct.sage')

Launching APFB processes $P_{j}$ for $j = 1, 2, 3$ .

We now explain how to launch an auxiliary APFB process.

These processes were designed to support $P_{0}$ and can be directed towards ongoing computations thanks to the variables text1 and text2.

We open a new sage session to make an APFB process join $P_{0}$ .

We first have to set :

text1 = str('precociousness')
text2 = str('evaporation')

The APFB will thus know that a battle is currently fought inside of the folder

and will thus know where they should go to join the fight!

A process number must be assigned to each APFB. For $P_{1}$ , we set

aux_number = 1

Since we want each APFB to be capable of mobilizing its own worker processes, we set

nb_workers = 8

We have to specify to each APFB the input data required to set up the initial environment for the case under study. Hence, we set :

INPUT_DATA=load('INPUT_DATA/DEMO/INPUT_DATA_DEMO_PFB.sobj')

The commands required to launch the APFB process $P_{1}$ are summarized below :

text1 = str('precociousness') # identification of the case under study
text2 = str('evaporation') # identification of the case under study
nb_workers = 8 # the APFB will be capable of mobilizing a pool of 8 workers
aux_number = 1 # depends on the number assigned to APFB process by the user
INPUT_DATA=load('INPUT_DATA/DEMO/INPUT_DATA_DEMO_PFB.sobj')
load('APFB_direct.sage')

Similarly, open new Sage console tabs, and proceed as follows to launch $P_{2}$ and $P_{3}$ :

Commands used to launch $P_{2}$ :

text1 = str('precociousness') 
text2 = str('evaporation')
nb_workers = 8 
aux_number = 2 # Process P_2
INPUT_DATA=load('INPUT_DATA/DEMO/INPUT_DATA_DEMO_PFB.sobj')
load('APFB_direct.sage')

Commands used to launch $P_{3}$ :

text1 = str('precociousness') 
text2 = str('evaporation')
nb_workers = 8 
aux_number = 3 # Process P_3
INPUT_DATA=load('INPUT_DATA/DEMO/INPUT_DATA_DEMO_PFB.sobj')
load('APFB_direct.sage')

Launching an extra APFB : Process $P_{4}$

To launch an extra APFB process whose purpose consists in getting ahead of the work to be done a the next iteration, the procedure is the same, except that we call for APFB_extra_direct instead of APFB_direct :

text1 = str('precociousness') 
text2 = str('evaporation')
nb_workers = 8 
aux_number = 4 # Process P_4
INPUT_DATA=load('INPUT_DATA/DEMO/INPUT_DATA_DEMO_PFB.sobj')
load('APFB_extra_direct.sage')